ΧβΡΩΡΎ»ί
“―÷ΣΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΝΫΕ®ΒψAΘ®-1Θ§0Θ©ΓΔBΘ®4Θ§0Θ©Θ§≈ΉΈοœΏy=ax2+bx-2Θ®aΓΌ0Θ©ΙΐΒψAΘ§BΘ§ΕΞΒψΈΣCΘ§ΒψPΘ®mΘ§nΘ©Θ®nΘΦ0Θ©ΈΣ≈ΉΈοœΏ…œ“ΜΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΚΆΕΞΒψCΒΡΉχ±ξΘΜ
Θ®2Θ©Β±ΓœAPBΈΣΕέΫ« ±Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©»τmΘΨ
Θ§Β±ΓœAPBΈΣ÷±Ϋ« ±Θ§ΫΪΗΟ≈ΉΈοœΏœρΉσΜρœρ”“ΤΫ“ΤtΘ®0ΘΦtΘΦ
Θ©ΗωΒΞΈΜΘ§ΒψCΓΔPΤΫ“ΤΚσΕ‘”ΠΒΡΒψΖ÷±πΦ«ΈΣCΓδΓΔPΓδΘ§ «Ζώ¥φ‘ΎtΘ§ ΙΒΟ ΉΈΜ“ά¥ΈΝ§Ϋ”AΓΔBΓΔPΓδΓΔCΓδΥυΙΙ≥…ΒΡΕύ±Ώ–ΈΒΡ÷ή≥ΛΉνΕΧΘΩ»τ¥φ‘ΎΘ§«σtΒΡ÷Β≤ΔΥΒΟς≈ΉΈοœΏΤΫ“ΤΒΡΖΫœρΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΚΆΕΞΒψCΒΡΉχ±ξΘΜ
Θ®2Θ©Β±ΓœAPBΈΣΕέΫ« ±Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©»τmΘΨ
| 3 |
| 2 |
| 5 |
| 2 |
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ¥ζ ΐΦΗΚΈΉέΚœΧβ,―Ι÷αΧβ,¥ΐΕ®œΒ ΐΖ®
Ζ÷ΈωΘΚΘ®1Θ©¥ΐΕ®œΒ ΐΖ®«σΫβΈω ΫΦ¥Ω…Θ§«σΒΟΫβΈω ΫΚσΉΣΜΜ≥…ΕΞΒψ ΫΦ¥Ω…Θ°
Θ®2Θ©“ρΈΣABΈΣ÷±ΨΕΘ§Υυ“‘Β±≈ΉΈοœΏ…œΒΡΒψP‘ΎΓ―CΒΡΡΎ≤Ω ±Θ§¬ζΉψΓœAPBΈΣΕέΫ«Θ§Υυ“‘-1ΘΦmΘΦ0Θ§Μρ3ΘΦmΘΦ4Θ°
Θ®3Θ©Ήσ”“ΤΫ“Τ ±Θ§ ΙAΓδD+DBΓεΉνΕΧΦ¥Ω…Θ§Ρ«Ο¥Ής≥ωΒψCΓδΙΊ”Ύx÷αΕ‘≥ΤΒψΒΡΉχ±ξΈΣCΓεΘ§ΒΟΒΫ÷±œΏPΓεCΓεΒΡΫβΈω ΫΘ§»ΜΚσΑ―AΒψΒΡΉχ±ξ¥ζ»κΦ¥Ω…Θ°
Θ®2Θ©“ρΈΣABΈΣ÷±ΨΕΘ§Υυ“‘Β±≈ΉΈοœΏ…œΒΡΒψP‘ΎΓ―CΒΡΡΎ≤Ω ±Θ§¬ζΉψΓœAPBΈΣΕέΫ«Θ§Υυ“‘-1ΘΦmΘΦ0Θ§Μρ3ΘΦmΘΦ4Θ°
Θ®3Θ©Ήσ”“ΤΫ“Τ ±Θ§ ΙAΓδD+DBΓεΉνΕΧΦ¥Ω…Θ§Ρ«Ο¥Ής≥ωΒψCΓδΙΊ”Ύx÷αΕ‘≥ΤΒψΒΡΉχ±ξΈΣCΓεΘ§ΒΟΒΫ÷±œΏPΓεCΓεΒΡΫβΈω ΫΘ§»ΜΚσΑ―AΒψΒΡΉχ±ξ¥ζ»κΦ¥Ω…Θ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏy=ax2+bx-2Θ®aΓΌ0Θ©ΙΐΒψAΘ§BΘ§
Γύ
Θ§
ΫβΒΟΘΚ
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=
x2-
x-2ΘΜ
ΓΏy=
x2-
x-2=
Θ®x-
Θ©2-
Θ§
ΓύCΘ®
Θ§-
Θ©Θ°
Θ®2Θ©»γΆΦ1Θ§“‘ABΈΣ÷±ΨΕΉς‘≤MΘ§‘ρ≈ΉΈοœΏ‘Ύ‘≤ΡΎΒΡ≤ΩΖ÷Θ§Ρή ΙΓœAPBΈΣΕέΫ«Θ§
ΓύMΘ®
Θ§0Θ©Θ§Γ―MΒΡΑκΨΕ=
Θ°
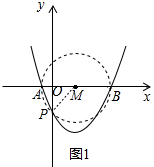
ΓΏPΓδ «≈ΉΈοœΏ”κy÷αΒΡΫΜΒψΘ§
ΓύOPΓδ=2Θ§
ΓύMPΓδ=
=
Θ§
ΓύPΓδ‘ΎΓ―M…œΘ§
ΓύPΓδΒΡΕ‘≥ΤΒψΘ®3Θ§-2Θ©Θ§
ΓύΒ±-1ΘΦmΘΦ0Μρ3ΘΦmΘΦ4 ±Θ§ΓœAPBΈΣΕέΫ«Θ°
Θ®3Θ©¥φ‘ΎΘΜ
≈ΉΈοœΏœρΉσΜρœρ”“ΤΫ“ΤΘ§“ρΈΣABΓΔPΓδCΓδ «Ε®÷ΒΘ§Υυ“‘AΓΔBΓΔPΓδΓΔCΓδΥυΙΙ≥…ΒΡΕύ±Ώ–ΈΒΡ÷ή≥ΛΉνΕΧΘ§÷Μ“ΣACΓδ+BPΓδΉν–ΓΘΜ
ΒΎ“Μ÷÷«ιΩωΘΚ≈ΉΈοœΏœρ”“ΤΫ“ΤΘ§ACΓδ+BPΓδΘΨAC+BPΘ§
ΒΎΕΰ÷÷«ιΩωΘΚœρΉσΤΫ“ΤΘ§»γΆΦ2Υυ ΨΘ§”…Θ®2Θ©Ω…÷ΣPΘ®3Θ§-2Θ©Θ§
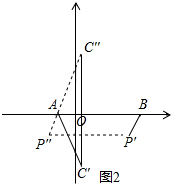
”÷ΓΏCΘ®
Θ§-
Θ©
ΓύC'Θ®
-tȧ-
ȩȧP'Ȯ3-tȧ-2ȩȧ
ΓΏAB=5Θ§
ΓύPΓεΘ®-2-tΘ§-2Θ©Θ§
“Σ ΙACΓδ+BPΓδΉνΕΧΘ§÷Μ“ΣACΓδ+APΓεΉνΕΧΦ¥Ω…Θ§
ΒψCΓδΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψCΓεΘ®
-tȧ
Θ©Θ§
…η÷±œΏPΓεCΓεΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
Θ§
ΫβΒΟ
Γύ÷±œΏy=
x+
t+
Θ§
ΒψA‘Ύ÷±œΏ…œΘ§
Γύ-
+
t+
=0
Γύt=
Θ°
Ι ΫΪ≈ΉΈοœΏœρΉσΤΫ“Τ
ΗωΒΞΈΜΝ§Ϋ”AΓΔBΓΔPΓδΓΔCΓδΥυΙΙ≥…ΒΡΕύ±Ώ–ΈΒΡ÷ή≥ΛΉνΕΧΘ°
Γύ
|
ΫβΒΟΘΚ
|
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=
| 1 |
| 2 |
| 3 |
| 2 |
ΓΏy=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
ΓύCΘ®
| 3 |
| 2 |
| 25 |
| 8 |
Θ®2Θ©»γΆΦ1Θ§“‘ABΈΣ÷±ΨΕΉς‘≤MΘ§‘ρ≈ΉΈοœΏ‘Ύ‘≤ΡΎΒΡ≤ΩΖ÷Θ§Ρή ΙΓœAPBΈΣΕέΫ«Θ§
ΓύMΘ®
| 3 |
| 2 |
| 5 |
| 2 |

ΓΏPΓδ «≈ΉΈοœΏ”κy÷αΒΡΫΜΒψΘ§
ΓύOPΓδ=2Θ§
ΓύMPΓδ=
| OP2+OM2 |
| 5 |
| 2 |
ΓύPΓδ‘ΎΓ―M…œΘ§
ΓύPΓδΒΡΕ‘≥ΤΒψΘ®3Θ§-2Θ©Θ§
ΓύΒ±-1ΘΦmΘΦ0Μρ3ΘΦmΘΦ4 ±Θ§ΓœAPBΈΣΕέΫ«Θ°
Θ®3Θ©¥φ‘ΎΘΜ
≈ΉΈοœΏœρΉσΜρœρ”“ΤΫ“ΤΘ§“ρΈΣABΓΔPΓδCΓδ «Ε®÷ΒΘ§Υυ“‘AΓΔBΓΔPΓδΓΔCΓδΥυΙΙ≥…ΒΡΕύ±Ώ–ΈΒΡ÷ή≥ΛΉνΕΧΘ§÷Μ“ΣACΓδ+BPΓδΉν–ΓΘΜ
ΒΎ“Μ÷÷«ιΩωΘΚ≈ΉΈοœΏœρ”“ΤΫ“ΤΘ§ACΓδ+BPΓδΘΨAC+BPΘ§
ΒΎΕΰ÷÷«ιΩωΘΚœρΉσΤΫ“ΤΘ§»γΆΦ2Υυ ΨΘ§”…Θ®2Θ©Ω…÷ΣPΘ®3Θ§-2Θ©Θ§

”÷ΓΏCΘ®
| 3 |
| 2 |
| 25 |
| 8 |
ΓύC'Θ®
| 3 |
| 2 |
| 25 |
| 8 |
ΓΏAB=5Θ§
ΓύPΓεΘ®-2-tΘ§-2Θ©Θ§
“Σ ΙACΓδ+BPΓδΉνΕΧΘ§÷Μ“ΣACΓδ+APΓεΉνΕΧΦ¥Ω…Θ§
ΒψCΓδΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψCΓεΘ®
| 3 |
| 2 |
| 25 |
| 8 |
…η÷±œΏPΓεCΓεΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
|
ΫβΒΟ
|
Γύ÷±œΏy=
| 41 |
| 28 |
| 41 |
| 28 |
| 13 |
| 14 |
ΒψA‘Ύ÷±œΏ…œΘ§
Γύ-
| 41 |
| 28 |
| 41 |
| 28 |
| 13 |
| 14 |
Γύt=
| 15 |
| 41 |
Ι ΫΪ≈ΉΈοœΏœρΉσΤΫ“Τ
| 15 |
| 41 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ¥ΐΕ®œΒ ΐΖ®«σΫβΈω ΫΘ§ΕΞΒψΉχ±ξΘ§Εΰ¥ΈΚ· ΐΒΡΕ‘≥Τ–‘Θ§“‘ΦΑΨύάκ÷°ΚΆΉν–ΓΒΡΈ ΧβΘ§…φΦΑΩΦΒψΫœΕύΘ§”–“ΜΕ®ΒΡΡ―Ε»Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
œ¬Ν–ΦΤΥψ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
AΓΔ
| ||||||
BΓΔΘ®
| ||||||
CΓΔ
| ||||||
DΓΔ
|
 »γΆΦΘ§ΓœAΘ§ΓœDΈΣ÷±Ϋ«Θ§AC”κDBœύΫΜ”ΎΒψEΘ§BE”κECœύΒ»Θ§‘ΎΆΦ÷–’“≥ωΝΫΕ‘»ΪΒ»»ΐΫ«–Έ≤ΔΥΒΟςάμ”…Θ°
»γΆΦΘ§ΓœAΘ§ΓœDΈΣ÷±Ϋ«Θ§AC”κDBœύΫΜ”ΎΒψEΘ§BE”κECœύΒ»Θ§‘ΎΆΦ÷–’“≥ωΝΫΕ‘»ΪΒ»»ΐΫ«–Έ≤ΔΥΒΟςάμ”…Θ° “―÷ΣΘΚΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2-Θ®m+3Θ©x+3=0”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ°
“―÷ΣΘΚΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2-Θ®m+3Θ©x+3=0”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ° ‘ΎΨΊ–ΈABCG÷–Θ§ΒψD «AGΒΡ÷–ΒψΘ§ΒψE «AB…œ“ΜΒψΘ§DEΓΆDCΘ§CEΫΜBD”ΎFΘ§
‘ΎΨΊ–ΈABCG÷–Θ§ΒψD «AGΒΡ÷–ΒψΘ§ΒψE «AB…œ“ΜΒψΘ§DEΓΆDCΘ§CEΫΜBD”ΎFΘ§