题目内容
20.计算:2sin45°-$\frac{1}{\sqrt{2}+1}$+sin225°+sin255°.分析 根据特殊角的三角函数值和三角形函数公式计算.
解答 解:原式=2×$\frac{\sqrt{2}}{2}$-($\sqrt{2}$-1)+sin225°+cos225°
=$\sqrt{2}$-$\sqrt{2}$+1+1
=2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了特殊角的三角函数值.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.若(-a2)•(-a)2•(-a)m>0,则( )
| A. | m为奇数 | B. | m为偶数 | C. | m为奇数且a>0 | D. | a>0,m为偶数 |
7.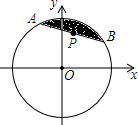 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )| A. | π-1 | B. | π-2 | C. | $\frac{4π}{3}$-1 | D. | $\frac{4π}{3}$-$\sqrt{3}$ |
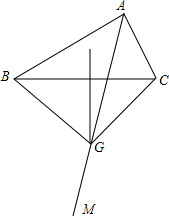 如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论.
如图,已知△ABC射线AM平分∠BAC,过BC的中点作垂线,与AM相交于点G,连接BG,CG,∠BAC和∠BGC的数量关系为互补,证明你的结论. 在由自然数排成的数阵中,在2016的正下方的自然数是多少?为什么?
在由自然数排成的数阵中,在2016的正下方的自然数是多少?为什么?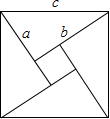 如图:这个图形被称为“弦图”,它是由四个全等的直角三角形拼成的正方形,你能用这个拼图验证勾股定理吗?
如图:这个图形被称为“弦图”,它是由四个全等的直角三角形拼成的正方形,你能用这个拼图验证勾股定理吗?