题目内容
在函数y=
(m为常数)的图象上有三点(3,y1),(1,y2),(-2,y3),则y1,y2,y3的大小关系是( )
| m2+1 |
| x |
| A、y3<y2<y1 |
| B、y1<y2<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:根据反比例函数图象上点的坐标特征,分别计算正自变量为3,1和-2的函数值,然后比较函数的大小即可.
解答:解:∵点(3,y1),(1,y2),(-2,y3)在函数y=
(m为常数)的图象,
∴y1=
,y2=
=m2+1,y3=
,
∴y3<y1<y2.
故选C.
| m2+1 |
| x |
∴y1=
| m2+1 |
| 3 |
| m2+1 |
| 1 |
| m2+1 |
| -2 |
∴y3<y1<y2.
故选C.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
相关题目
下列数轴画正确的是( )
A、 |
B、 |
C、 |
D、 |
一客轮船长江从A港顺流到达B港需6小时,从B港逆流到A港需8小时,一天,客轮从A港出发开往B港,2小时后,客轮上的一位旅客的帽子不慎落入江中,则帽子漂流到B港需要( )小时.
| A、48 | B、32 | C、28 | D、24 |
下列结论中,有( )个是错误的.
①-a<0 ②-a<a ③-a≠a ④-a≠0.
①-a<0 ②-a<a ③-a≠a ④-a≠0.
| A、4 | B、3 | C、2 | D、1 |
 如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=
如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=| 6 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
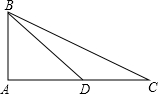 已知:如图,在△ABC中,∠A=90°,点D在边AC上,若∠ADB=45°,tan∠C=
已知:如图,在△ABC中,∠A=90°,点D在边AC上,若∠ADB=45°,tan∠C=


