Question

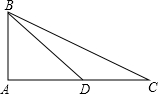已知：如图，在△ABC中，∠A=90°，点D在边AC上，若∠ADB=45°，tan∠C=

1

2

，AD=10．
（1）求DC的长；
（2）求tan∠DBC的值．

Answer 1

考点：解直角三角形

专题：计算题

分析：（1）在Rt△ABC中，由∠A=90°，∠ADB=45°可得AD=AB=10，再利用正切的定义可计算出AC=2AB=20，所以DC=AC-AD=10；
（2）过点D作DE⊥BC于点E，如图，先利用勾股定理计算出在BD=

2

AD=10

2

，BC=10

5

，在利用面积法得到S_△BCD=

1

2

DE•BC=

1

2

CD•AB，则可计算出DE=2

5

，接着在Rt△BDE中根据勾股定理计算出BE=6

5

，然后根据正切的定义求解．

解答：解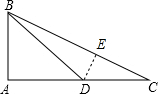：（1）在Rt△ABC中，∵∠A=90°，∠ADB=45°，
∴∠ABD=45°，
∴AD=AB=10，
∵tan∠C=

AB

AC

=

1

2

，
∴AC=2AB=20，
∴DC=AC-AD=20-10=10；
（2）过点D作DE⊥BC于点E，如图，
在Rt△ABD中，BD=

2

AD=10

2

，
在Rt△ABC中，∵AB=10，AC=20，
∴BC=

AB2+AC2

=10

5

，
∵S_△BCD=

1

2

DE•BC=

1

2

CD•AB，
∴DE=

10×10

10 5

=2

5

，
在Rt△BDE中，∵BD=10

2

，DE=2

5

，
∴BE=

BD2-DE2

=6

5

，
∴tan∠DBE=

DE

BE

=

2 5

6 5

=

1

3

，
即tan∠DBC的值=

1

3

．

点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了三角形面积公式．