题目内容
如图，在边长都是1的正方体纸箱的外部，一只蚂蚁从顶点A沿纸箱表面爬到顶点B点，那么它所行的最短路线的长是考点：平面展开-最短路径问题
专题：
分析：把此正方体的一面展开，然后在平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于棱长，另一条直角边长等于两条棱长，利用勾股定理可求得．
解答：解：∵展开后由勾股定理得：AB2=12+（1+1）2=5，
∴AB=
．
故答案为：
．
∴AB=
| 5 |
故答案为：
| 5 |
点评：本题考查了平面展开-最短路径问题，“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
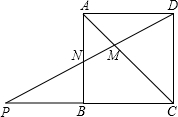如图，正方形ABCD中，点N为AB的中点，连接DN并延长交CB的延长线于点P，连接AC交DN于点M．若PN=3，则DM的长为
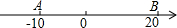如图A、B两点在数轴上分别表示-10和20，动点P从点A出发以10个单位每秒的速度向右运动，动点Q从点B出发以每秒5个单位的速度出向右运动．设运动时间为t．
如图，已知∠A=∠E，∠C=∠D，EC=AD，求证：∠1=∠2．已知抛物线y=ax2+bx+c与x轴的一个交点为（1，0），对称轴为直线x=-1，则该抛物线与x轴另一个交点坐标为（ ）
| A、（-3，0） |
| B、（-2，0） |
| C、（2，0） |
| D、无法确定 |
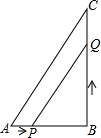如图，△ABC中，∠B=90°，AB=6，BC=8，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当Q运动到C点时停止运动，P点也随之停止运动，如果点P、Q分别从点A、B同时出发．