题目内容
如图，已知∠A=∠E，∠C=∠D，EC=AD，求证：∠1=∠2．考点：全等三角形的判定与性质
专题：证明题
分析：利用ASA得到三角形ABD与三角形EBC全等，利用全等三角形对应角相等得到∠ABD=∠EBC，利用等式的性质变形即可得证．
解答：证明：在△ABD和△EBC中，
，
∴△ABD≌△EBC（ASA），
∴∠ABD=∠EBC，即∠1+∠EBD=∠2+∠EBD，
则∠1=∠2．
|
∴△ABD≌△EBC（ASA），
∴∠ABD=∠EBC，即∠1+∠EBD=∠2+∠EBD，
则∠1=∠2．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
如图，在边长都是1的正方体纸箱的外部，一只蚂蚁从顶点A沿纸箱表面爬到顶点B点，那么它所行的最短路线的长是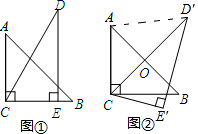
一副三角板如图①放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°斜边AB=4，CD=5．把三角板DCE绕着点C顺时针旋转15°得到△D′CE′（如图②），此时AB与CD′交于点O，则cos∠OAD′=
如图，已知∠CAB=∠DBA 要使△ABC≌△BAD，只要增加的一个条件是