题目内容
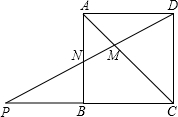 如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为
如图,正方形ABCD中,点N为AB的中点,连接DN并延长交CB的延长线于点P,连接AC交DN于点M.若PN=3,则DM的长为考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:
分析:因为PN=3,又易知△PBN全等于△DNA,所以DN=PN=3,又因为AB∥DC,所以易证△AMN相似与△CMD,所以NM:DM=AN:DC=
,又PN=3,可求得DM.
| 1 |
| 2 |
解答:解:∵四边形ABCD为正方形,N为中点,
∴AD=PB,AN=BN,∠DAN=∠PBN=90°,
在△PBN和△DNA中
∴△PBN≌△DNA(SAS),
∴DN=PN=3,即DM+MN=3,
∵AB∥CD,
∴△AMN∽△CMD,
∴
=
=
,
∴DM=2,
故答案为:2.
∴AD=PB,AN=BN,∠DAN=∠PBN=90°,
在△PBN和△DNA中
|
∴△PBN≌△DNA(SAS),
∴DN=PN=3,即DM+MN=3,
∵AB∥CD,
∴△AMN∽△CMD,
∴
| MN |
| MD |
| AN |
| DC |
| 1 |
| 2 |
∴DM=2,
故答案为:2.
点评:本题主要考查全等三角形、相似三角形的判定和性质,由条件证得DN=3和MN:MD=1:2是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果3x2myn与-5x4y3是同类项,则m和n的取值是( )
| A、3和-2 | B、-3和2 |
| C、2和3 | D、-3和-2 |
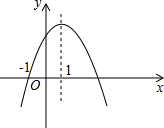 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论: 如图,在边长都是1的正方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B点,那么它所行的最短路线的长是
如图,在边长都是1的正方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B点,那么它所行的最短路线的长是 二次函数y=ax2+bx+c(a≠0)的部分图象如图,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,根据图象解答下列问题: