��Ŀ����
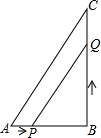 ��ͼ����ABC�У���B=90�㣬AB=6��BC=8����P�ӵ�A��ʼ��AB�����B��1cm/s���ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2cm/s���ٶ��ƶ�����Q�˶���C��ʱֹͣ�˶���P��Ҳ��ֹ֮ͣ�˶��������P��Q�ֱ�ӵ�A��Bͬʱ������
��ͼ����ABC�У���B=90�㣬AB=6��BC=8����P�ӵ�A��ʼ��AB�����B��1cm/s���ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2cm/s���ٶ��ƶ�����Q�˶���C��ʱֹͣ�˶���P��Ҳ��ֹ֮ͣ�˶��������P��Q�ֱ�ӵ�A��Bͬʱ��������1�����������ӣ���PBQ���������8ƽ�����ף�
��2����PCQ������ܵ���12.6ƽ�����ף�
��3�����������ӣ���PBQ��������������Ϊ����ƽ�����ף�
���㣺һԪ���η��̵�Ӧ��,���κ�������ֵ
ר�⣺���ζ�������
��������1���辭��x���PBQ���������8ƽ�����ף�AP=x��BQ=2x��BP=6-x���������ε������ʽ�������������⼴�ɣ�
��2����CQ=8-2x��PB=6-x���������ε������ʽ�������������⼴�ɣ�
��3�����PBQ�����Ϊs���������ε������ʽ��ʾ��s��x�Ĺ�ϵʽ�����ɺ��������ʾͿ���������ۣ�
��2����CQ=8-2x��PB=6-x���������ε������ʽ�������������⼴�ɣ�
��3�����PBQ�����Ϊs���������ε������ʽ��ʾ��s��x�Ĺ�ϵʽ�����ɺ��������ʾͿ���������ۣ�
����⣺��1���辭��x���PBQ���������8ƽ�����ף�AP=x��BQ=2x��BP=6-x�������⣬��
=8��
��ã�x1=2��x2=4��
���辭��2���4�룬��PBQ���������8ƽ�����ף�
��2����x����PCQ������ܵ���12.6ƽ�����ף������⣬��
=12.6��
��������
5x2-50x+32=0
���=2500-20��32��0
��ԭ�����н⣬
���PCQ������ܵ���12.6ƽ�����ף�
��3�����PBQ�����Ϊs�������⣬��
s=
=-x2+6x��
s=��x-3��2+9��
��a=-1��0��
�൱x=3ʱ��s���=9��
�𣺹�3���ӣ���PBQ��������������Ϊ9ƽ�����ף�
| 2x(6-x) |
| 2 |
��ã�x1=2��x2=4��
���辭��2���4�룬��PBQ���������8ƽ�����ף�
��2����x����PCQ������ܵ���12.6ƽ�����ף������⣬��
| (6-x)(8-2x) |
| 2 |
��������
5x2-50x+32=0
���=2500-20��32��0
��ԭ�����н⣬
���PCQ������ܵ���12.6ƽ�����ף�
��3�����PBQ�����Ϊs�������⣬��
s=
| 2x(6-x) |
| 2 |
s=��x-3��2+9��
��a=-1��0��
�൱x=3ʱ��s���=9��
�𣺹�3���ӣ���PBQ��������������Ϊ9ƽ�����ף�
���������⿼������һԪ���η��̽�ʵ����������ã�һԪ���η��̵Ľⷨ�����ã������б�ʽ�����ã������ε������ʽ�����ã����κ��������ʵ����ã����ʱ���������ε������ʽ���������ϵʽ�ǹؼ���

��ϰ��ϵ�д�
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
�����Ŀ
������һԪһ�η��̵��ǣ�������
| A��2x+y=1 |
| B��x2+1=0 |
| C��2x=1 |
| D��xy=1 |
��
��
��
��
��a+
�з�ʽ�У�������
| 1 |
| x |
| 1 |
| 2 |
| x2+1 |
| 2 |
| a |
| x+y |
| 1 |
| m |
| A��2�� | B��3�� | C��4�� | D��5�� |
 ��ͼ���ڱ߳�����1��������ֽ����ⲿ��һֻ���ϴӶ���A��ֽ�������������B�㣬��ô�����е����·�ߵij���
��ͼ���ڱ߳�����1��������ֽ����ⲿ��һֻ���ϴӶ���A��ֽ�������������B�㣬��ô�����е����·�ߵij��� ���κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ������ͼ�����������⣺
���κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ������ͼ�����������⣺ ��ͼ����֪��CAB=��DBA Ҫʹ��ABC�ա�BAD��ֻҪ���ӵ�һ��������
��ͼ����֪��CAB=��DBA Ҫʹ��ABC�ա�BAD��ֻҪ���ӵ�һ��������