题目内容
7.设△ABC的内切圆半径为r,BC=a,AC=b,AB=c,且其上的高分别为ha,hb,hc满足ha+hb+hc=9r.则△ABC的形状为等边三角形.分析 根据三角形的面积公式得到S△ABC=$\frac{1}{2}$(a+b+c)r=$\frac{1}{2}$a•ha=$\frac{1}{2}$b•hb=$\frac{1}{2}$c•hc,推出ha=$\frac{1}{a}$(a+b+c)r,同理hb=$\frac{1}{b}$(a+b+c)r,hc=$\frac{1}{c}$(a+b+c)r,列方程得到a=b=c,于是得到结论.
解答 解:∵S△ABC=$\frac{1}{2}$(a+b+c)r=$\frac{1}{2}$a•ha=$\frac{1}{2}$b•hb=$\frac{1}{2}$c•hc,
∴ha=$\frac{1}{a}$(a+b+c)r,
同理hb=$\frac{1}{b}$(a+b+c)r,hc=$\frac{1}{c}$(a+b+c)r,
∴ha+hb+hc=(a+b+c) r($\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$)=9r,
∴(a+b+c)($\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$)=3+($\frac{b}{a}$+$\frac{a}{b}$)+($\frac{a}{c}$+$\frac{c}{a}$)+($\frac{b}{c}$+$\frac{c}{b}$)≥3+2+2+2=9,当且仅当a=b=c时等号成立,
∴a=b=c,
∴△ABC的形状为等边三角形.
故答案为:等边三角形.
点评 本题考查了三角形的内切圆与内心,等式的性质,三角形面积公式,熟练掌握三角形的面积的计算方法是解题的关键.

练习册系列答案
相关题目
 B. 60.9×105 C. 609×104 D. 6.09×105
B. 60.9×105 C. 609×104 D. 6.09×105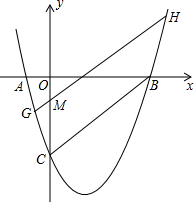 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于G、H(G左H右),若点M在y轴上运动,试判断HM-CM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于G、H(G左H右),若点M在y轴上运动,试判断HM-CM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
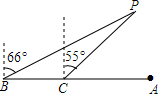 黄岩岛海域历来就是中国渔民的传统捕鱼场所,但黄岩岛附近暗礁众多,稍不留神,就有搁浅的危险.例如,露出水面的一块礁石P附近160米以内就有暗礁.一日,一艘渔船误入该暗礁区域后,费了九牛二虎之力,终于到到了安全地带,但在点A处时渔船突然熄火,经检查,原来柴油耗尽,此时,位于附近点B处的一艘中国渔政船收到求救信号前往送油,经观测,渔船所在位置A恰好在B处的正东方向,而礁石P在B处的北偏东66°方向,渔政船朝正东方向航行150米到C处时测得P位于北偏东55°方向.问:渔政船如果继续向正东方向航行,有无触礁的危险?
黄岩岛海域历来就是中国渔民的传统捕鱼场所,但黄岩岛附近暗礁众多,稍不留神,就有搁浅的危险.例如,露出水面的一块礁石P附近160米以内就有暗礁.一日,一艘渔船误入该暗礁区域后,费了九牛二虎之力,终于到到了安全地带,但在点A处时渔船突然熄火,经检查,原来柴油耗尽,此时,位于附近点B处的一艘中国渔政船收到求救信号前往送油,经观测,渔船所在位置A恰好在B处的正东方向,而礁石P在B处的北偏东66°方向,渔政船朝正东方向航行150米到C处时测得P位于北偏东55°方向.问:渔政船如果继续向正东方向航行,有无触礁的危险?