题目内容
14.把下列多项式,在实数范围内因式分解①x2-2
②x2-2$\sqrt{3}$x+3
③a2-9a.
分析 ①将2写成($\sqrt{2}$)2,运用平方差公式分解;
②将3写成($\sqrt{3}$)2,运用完全平方公式分解;
③提取公式a即可分解.
解答 解:①原式=x2-($\sqrt{2}$)2=(x+$\sqrt{2}$)(x-$\sqrt{2}$);
②原式=x2-2•x•$\sqrt{3}$+($\sqrt{3}$)2=(x-$\sqrt{3}$)2;
③原式=a(a-9).
点评 本题主要考查因式分解的能力,当一个多项式有公因式,将其分解因式时应先提取公因式,再对余下的多项式根据公式继续分解.当要求在实数范围内进行因式分解时,分解的式子的结果一般要分到出现无理数为止.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.等腰三角形顶角是120°,则一腰上的高与另一腰的夹角的度数为( )
| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
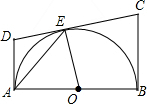 如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )
如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )
 B.
B. 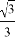 C.
C. 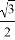 D.
D. 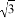
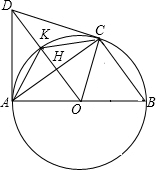 AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.
AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.