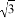题目内容
2.O为直线AB上一点,过点O向直线AB上方作射线OC,且∠AOC=30°,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的上方,现将三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.(1)经过1秒,OM恰好平分∠BOC,求t的值.
(2)在(1)的条件下,ON是否平分∠AOC?请说明理由.
(3)在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC平分∠MON?请说明理由.
(4)在(3)的条件下,经过多长时间OC平分∠MOB?请画图并说明理由.
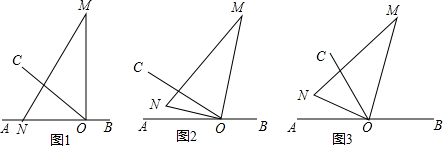
分析 (1)根据∠AOC=30°、OM恰好平分∠BOC知∠BOM=75°,进而可知旋转的度数,结合旋转速度可得时间t;
(2)根据图形和题意得出∠AON+∠BOM=90°,∠CON+∠COM=90°,再根据∠BOM=∠COM,即可得出ON平分∠AOC;
(3)根据图形和题意得出∠AON+∠BOM=90°,∠CON=∠COM=45°,再根据转动速度从而得出答案;
(4)分别根据转动速度关系和OC平分∠MOB画图即可.
解答 解:(1)∵∠AON+∠BOM=90°,∠COM=∠MOB,
∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC-∠CON=30°-15°=15°,
解得:t=15°÷3°=5秒;
(2)是,理由如下:
∵∠CON=15°,∠AON=15°,
∴ON平分∠AOC;
(3)5秒时OC平分∠MON,理由如下:
∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∵∠AOC-∠AON=45°,
可得:6t-3t=15°,
解得:t=5秒;
(4)OC平分∠MOB
∵∠AON+∠BOM=90°,∠BOC=∠COM,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∴∠COM为$\frac{1}{2}$(90°-3t),
∵∠BOM+∠AON=90°,
可得:180°-(30°+6t)=$\frac{1}{2}$(90°-3t),
解得:t=$\frac{70}{3}$秒;
如图: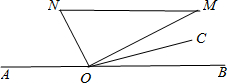
点评 此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | -2 | B. | 0 | C. | $\frac{1}{3}$ | D. | $\sqrt{3}$ |
 与
与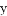 轴交于点A,与反比例函数
轴交于点A,与反比例函数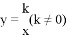 的图像交于点C,过点C作CB⊥
的图像交于点C,过点C作CB⊥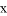 轴于点B,AO=3BO,则反比例函数的解析式为( )
轴于点B,AO=3BO,则反比例函数的解析式为( )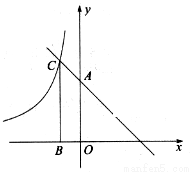
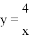 B.
B. 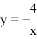 C.
C. 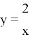 D.
D. 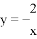
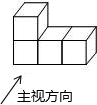 如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积.
如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积. 从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱.
从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱.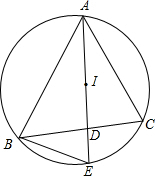 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.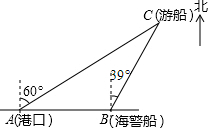 如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时) B.
B. 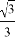 C.
C. 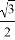 D.
D.