题目内容
12．
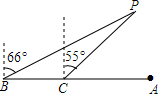黄岩岛海域历来就是中国渔民的传统捕鱼场所，但黄岩岛附近暗礁众多，稍不留神，就有搁浅的危险．例如，露出水面的一块礁石P附近160米以内就有暗礁．一日，一艘渔船误入该暗礁区域后，费了九牛二虎之力，终于到到了安全地带，但在点A处时渔船突然熄火，经检查，原来柴油耗尽，此时，位于附近点B处的一艘中国渔政船收到求救信号前往送油，经观测，渔船所在位置A恰好在B处的正东方向，而礁石P在B处的北偏东66°方向，渔政船朝正东方向航行150米到C处时测得P位于北偏东55°方向．问：渔政船如果继续向正东方向航行，有无触礁的危险？
分析 过P作PD⊥AB于D，解直角三角形得到BD=$\frac{PD}{tan24°}$，CD=$\frac{PD}{tan35°}$，列方程即可得到结论．
解答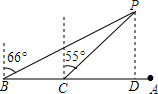 
解：过P作PD⊥AB于D，根据题意得：∠PBC=24°，∠PCD=35°，BC=150米，
在Rt△PBD中，BD=$\frac{PD}{tan24°}$，
在Rt△PCD中，CD=$\frac{PD}{tan35°}$，
∵BC=BD-CD=$\frac{PD}{tan24°}$-$\frac{PD}{tan35°}$=$\frac{PD}{0.4452}$-$\frac{PD}{0.7}$=150，
∴PD≈122.5＜160米，
∴有触礁的危险．
点评 此题主要考查了方向角的应用，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
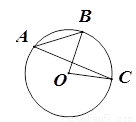
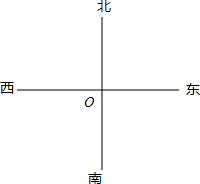甲、乙两船同时从小岛O出发，甲船速度为40海里/时，沿北偏西20°的方向航行；乙船沿北偏东70°的方向，以30海里/时的速度航行，半小时后甲、乙两船分别到达A，B两处．
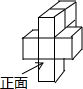如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面图是由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（ ）
