题目内容
15.已知抛物线 y=2x2-4x-6.(1)配方,画出它的图象;
(2)在图中标出它的对称轴与x轴、y轴的交点坐标.
分析 (1)首先把抛物线的解析式配方,可得到其顶点坐标以及对称轴,再分别求出抛物线和坐标轴的交点即可画出函数的图象;
(2)由(1)的作图过程即可得到它的对称轴与x轴、y轴的交点坐标.
解答 解:
(1)、(2)设y=0,则x=3或-1,所以抛物线和x轴的交点坐标是(3,0)和(-1,0);
设x=0,则y=-3,所以抛物线和y轴的交点坐标是(0,-3),
函数配方得:y=2(x-1)2-8;
函数图象如图所示: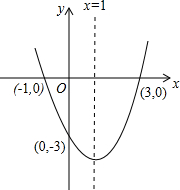
点评 本题考查了求抛物线的和坐标轴的交点坐标问题以及画函数图象,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
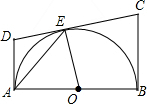 如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )
如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( ) 甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处.
甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处. 从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱.
从正面、左面、上面看到的某物体的形状如图所示,则该物体为三棱柱.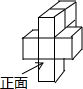 如果用□表示1个立方体,用
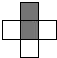
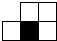
如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )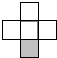


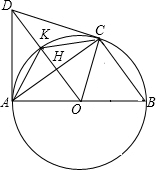 AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.
AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.