题目内容
8.在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,以PB为边作等边△PBM,则线段AM的长最大值为5.分析 分情况讨论,当点P在第一象限内时,将△APM绕着点P顺时针旋转60°得△DPB,连接AD,根据旋转的性质求得AM的最大值为5,当点P在第四象限内时,同理可得线段AM的长最大值为5.
解答 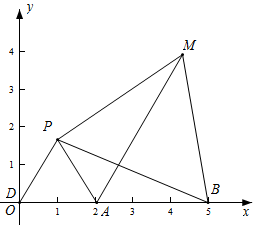 解:如图,当点P在第一象限内时,将△APM绕着点P顺时针旋转60°得△DPB,连接AD,则
解:如图,当点P在第一象限内时,将△APM绕着点P顺时针旋转60°得△DPB,连接AD,则
DP=AP,∠APD=60°,AM=BD,
∴△ADP是等边三角形,
∴由BD≤AD+AB可得,当D在BA的延长线上时,BD最长,
此时,点D与点O重合,
又∵点A的坐标为(2,0),点B的坐标为(5,0),
∴AB=5-2=3,AD=AO=2,
∴BD=AD+AB=2=3=5=AM,
即线段AM的长最大值为5;
当点P在第四象限内时,同理可得线段AM的长最大值为5.
故答案为:5.
点评 本题主要考查了等边三角形的性质,最大值问题以及旋转的性质,正确作出辅助线构造全等三角形是解题的关键,解题时注意分类思想的运用.

练习册系列答案
相关题目
 如图,带箭头的两条直线互相平行,其中一条直线经过正五边形的一个顶点,若∠1=45°,则∠2=27°.
如图,带箭头的两条直线互相平行,其中一条直线经过正五边形的一个顶点,若∠1=45°,则∠2=27°. 如图,在△ABC中,点D、E在边AB上,点F在边AC上,且AD=DE=EB,DF∥BC,设$\overrightarrow{EB}$=$\overrightarrow{a}$,$\overrightarrow{EC}$=$\overrightarrow{b}$,则用$\overrightarrow{a}、\overrightarrow{b}$表示$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$.
如图,在△ABC中,点D、E在边AB上,点F在边AC上,且AD=DE=EB,DF∥BC,设$\overrightarrow{EB}$=$\overrightarrow{a}$,$\overrightarrow{EC}$=$\overrightarrow{b}$,则用$\overrightarrow{a}、\overrightarrow{b}$表示$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$. 如图,在⊙O中,半径OB⊥OE于点O,过OB的中点作MN∥OE交⊙O于点M,N,则$\widehat{ME}$的度数为150°.
如图,在⊙O中,半径OB⊥OE于点O,过OB的中点作MN∥OE交⊙O于点M,N,则$\widehat{ME}$的度数为150°.