题目内容
3．在实数范围内因式分解：（x2+x）2-1=（x2+x+1）（x-$\frac{-1+\sqrt{5}}{2}$）（x-$\frac{-1-\sqrt{5}}{2}$）．分析 原式利用平方差公式分解即可．
解答 解：原式=（x2+x+1）（x2+x-1）=（x2+x+1）（x-$\frac{-1+\sqrt{5}}{2}$）（x-$\frac{-1-\sqrt{5}}{2}$），
故答案为：（x2+x+1）（x-$\frac{-1+\sqrt{5}}{2}$）（x-$\frac{-1-\sqrt{5}}{2}$）
点评 此题考查了实数范围内分解因式，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．
如图，点P在∠AOB的平分线上，PC⊥OA于点C，PC=1，点Q是射线OB上的一个动点，线段PQ长度的最小值为a，下列说法正确的是（ ）
如图，点P在∠AOB的平分线上，PC⊥OA于点C，PC=1，点Q是射线OB上的一个动点，线段PQ长度的最小值为a，下列说法正确的是（ ）| A． | a＞1 | B． | a=1 | C． | a＜1 | D． | 以上都有可能 |
如图，P为⊙O的直径AB延长线上的一点，PC切⊙O于点C，弦CD⊥AB，垂足为点E，若PC=3，PB=2．则圆的半径为$\frac{5}{4}$．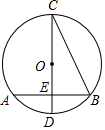
如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=4$\sqrt{2}$，∠BCD=30°，则⊙O的半径为$\frac{4\sqrt{6}}{3}$．