题目内容
19.已知点(-1,y1),(2,y2),(3,y3)在反比例函数y=$\frac{-{k}^{2}-1}{x}$的图象上,则用“<”连接y1,y2,y3为y2<y3<y1.分析 先根据反比例函数中k<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解答 解:∵反比例函数y=$\frac{-{k}^{2}-1}{x}$中,-k2-1<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大,
∵-1<0,
∴点A(-1,y1)位于第二象限,
∴y1>0;
∵0<2<3,
∴B(1,y2)、C(2,y3)在第四象限,
∵2<3,
∴y2<y3<0,
∴y2<y3<y1.
故答案为:y2<y3<y1.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
10.某篮球队员共16人,每人投篮6次,投进球数的次数分配如表所示.
若此队投进球的中位数是2.5,则众数是2.
| 投进球数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 次数(人) | 1 | 2 | x | y | 3 | 2 | 2 |
4. 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )| A. | 2和1 | B. | 1.25和1 | C. | 1和1 | D. | 1和1.25 |
11. 如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
 如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
如图,直线a、b被直线c所截,下列条件能使a∥b的是( )| A. | ∠1=∠6 | B. | ∠2=∠6 | C. | ∠1=∠3 | D. | ∠5=∠7 |
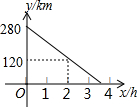 甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h
甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h