题目内容
解分式方程的基本思想是把分式方程化为_________,最后要注意_________.
 整式方程 检验
【解析】解分式方程的基本思想是把分式方程化为整式方程,最后要注意检验,
故答案为:整式方程,检验.
整式方程 检验
【解析】解分式方程的基本思想是把分式方程化为整式方程,最后要注意检验,
故答案为:整式方程,检验.
练习册系列答案
相关题目
已知二次函数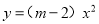 的图象开口向下,则m的取值范围是________
的图象开口向下,则m的取值范围是________
 m<2
【解析】由二次函数的图象的开口方向,知m-2<0,确定m的取值范围m<2.
故答案为:m<2.
m<2
【解析】由二次函数的图象的开口方向,知m-2<0,确定m的取值范围m<2.
故答案为:m<2. 将二次函数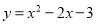 化成
化成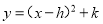 形式,则h+k结果为( )
形式,则h+k结果为( )
A. -5
B. 5
C. -3
D. 3
 C
【解析】.
则h=1,k=-4,
∴h+k=-3.
故选:C.
C
【解析】.
则h=1,k=-4,
∴h+k=-3.
故选:C. 一项工作,若甲单独完成需x小时,则甲每小时完成工作的________.若甲、乙合作 需8小时完成,则乙每小时完成工作的_______.
 【解析】一项工作,若甲单独完成需x小时,则甲每小时完成工作的,
若甲、乙合作需8小时完成,则乙每小时完成工作的,
故答案为: , .
【解析】一项工作,若甲单独完成需x小时,则甲每小时完成工作的,
若甲、乙合作需8小时完成,则乙每小时完成工作的,
故答案为: , . 若分式方程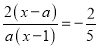 的解为x=3,则a的值为_______.
的解为x=3,则a的值为_______.
 5
【解析】由题意得: ,
解得:a=5,
经检验a=5符合原方程,
故答案为:5.
5
【解析】由题意得: ,
解得:a=5,
经检验a=5符合原方程,
故答案为:5. 如图所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
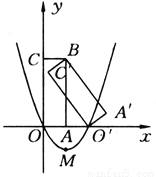
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
 (1) y=x2-2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析:(1)如图2-83所示,连...
(1) y=x2-2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析:(1)如图2-83所示,连... 如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点p的横坐标是4,图象与x轴交于点A(m,0)和点B,且点A在点B的左侧,那么线段AB的长是____.(用含字母m的代数式表示)
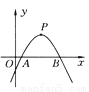
 8-2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4,
所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A.B两点关于对称轴对称,
因为点A(m,0),且m<4,即AD=4-m,
所以AB=2AD=2(4-m)=8-2m,
故答案为:8-2m.
8-2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4,
所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A.B两点关于对称轴对称,
因为点A(m,0),且m<4,即AD=4-m,
所以AB=2AD=2(4-m)=8-2m,
故答案为:8-2m. 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行 海里可使渔船到达离灯塔距离最近的位置.
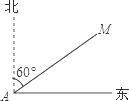
 .
【解析】试题解析:如图,过M作东西方向的垂线,设垂足为N.
易知:∠MAN=90°=30°.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,
∴AN=AM•cos∠MAN=100×=海里.
故该船继续航行海里可使渔船到达离灯塔距离最近的位置.
.
【解析】试题解析:如图,过M作东西方向的垂线,设垂足为N.
易知:∠MAN=90°=30°.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,
∴AN=AM•cos∠MAN=100×=海里.
故该船继续航行海里可使渔船到达离灯塔距离最近的位置. 如图,在?ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
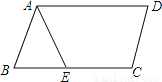
A.8cm B.6cm C.4cm D.2cm
 C
【解析】
试题分析:【解析】
∵四边形ABCD是平行四边形,
∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BEA=∠BAE,
∴BE=AB=8cm,
∴CE=BC﹣BE=4cm;
故答案为:C.
C
【解析】
试题分析:【解析】
∵四边形ABCD是平行四边形,
∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BEA=∠BAE,
∴BE=AB=8cm,
∴CE=BC﹣BE=4cm;
故答案为:C. 
