题目内容
7. 如图,已知BC⊥CD,∠1=∠2=∠3.
如图,已知BC⊥CD,∠1=∠2=∠3.(1)试判断AC与BD的位置关系,为什么?
(2)若∠4=70°,∠5=∠6.求∠ABC的度数.
分析 (1)根据垂直的定义得出∠1+∠2=90°,由∠1=∠2=∠3,再得出∠1+∠3=90°,即可得出AC⊥BD;
(2)根据∠4的度数得出∠5,由∠5=∠6,即可得出∠ABO,由外角的性质即可得出∠ABC=∠ABO+∠OBC.
解答 解:(1)AC⊥BD,
原因:∵BC⊥CD,
∴∠1+∠2=90°,
又∵∠1=∠2=∠3,
∴∠1+∠3=90°,
∴∠COD=90°,
∴AC⊥BD;
(2)∵∠4=70°,
∴∠5=20°,
∵∠5=∠6,
∴∠6=20°,
∴∠ABO=70°,
∵∠ABC=∠ABO+∠OBC,
∴∠ABC=70°+45°=115°.
点评 本题考查了垂线,以及垂直的定义,是基础知识要熟练掌握.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
18. 如图,如果∠AFE+∠FED=180°,那么( )
如图,如果∠AFE+∠FED=180°,那么( )
 如图,如果∠AFE+∠FED=180°,那么( )
如图,如果∠AFE+∠FED=180°,那么( )| A. | AC∥DE | B. | AB∥FE | C. | ED∥AB | D. | EF∥AC |
9.△ABC中,AB=2,AC=x,中线AD=4,则x的值可能是( )
| A. | 12 | B. | 14 | C. | 16 | D. | 8 |
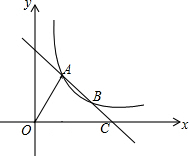 如图,直线AB交双曲线y=$\frac{k}{x}$于点A,B,交x轴于点C,连结OA,若OA⊥AB,tan∠ACO=$\frac{1}{2}$,S△OAC=12,则k的值为$\frac{24}{5}$.
如图,直线AB交双曲线y=$\frac{k}{x}$于点A,B,交x轴于点C,连结OA,若OA⊥AB,tan∠ACO=$\frac{1}{2}$,S△OAC=12,则k的值为$\frac{24}{5}$. 如图,点M是线段AB的中点,N在MB上,MN=$\frac{2}{5}$AM,若AM=15cm.求线段NB的长.
如图,点M是线段AB的中点,N在MB上,MN=$\frac{2}{5}$AM,若AM=15cm.求线段NB的长.