题目内容
9.△ABC中,AB=2,AC=x,中线AD=4,则x的值可能是( )| A. | 12 | B. | 14 | C. | 16 | D. | 8 |
分析 延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系即可求解.
解答 解:延长AD至E,使DE=AD,连接CE. ∵AD是△ABC的中线,
∵AD是△ABC的中线,
∴BD=CD,
在△ADB和△EDC中$\left\{\begin{array}{l}{AD=ED}\\{∠ADB=∠EDC}\\{DB=DC}\end{array}\right.$,
∴△ABD≌△ECD(SAS),
∴CE=AB.
在△ACE中,8-2=6<x<8+2=10,
故选D
点评 此题综合运用了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.

练习册系列答案
相关题目
4.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.若(x-1)0=1,求x的取值范围( )
| A. | x≤1 | B. | x≥1 | C. | x≠1 | D. | x=1 |
 如图,已知BC⊥CD,∠1=∠2=∠3.
如图,已知BC⊥CD,∠1=∠2=∠3.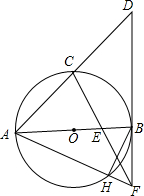 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,连结AC并延长到点D,使AC=CD,E是OB的中点,连结CE并延长交DB于点F.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,连结AC并延长到点D,使AC=CD,E是OB的中点,连结CE并延长交DB于点F.