题目内容
1.计算:(1)${(\frac{1}{2})^{-1}}+{(π-2017)^0}-{(-1)^{2017}}$
(2)(-a)3•a2+(2a4)2÷a3.
分析 (1)直接利用负指数幂的性质以及零指数幂的性质和有理数的成芳运算法则计算得出答案;
(2)直接利用积的乘方运算法则和同底数幂的乘除运算法则、整式的除法运算法则计算得出答案.
解答 解:(1)原式=2+1-(-1)
=4;
(2)原式=-a5+4a8÷a3
=3a5.
点评 此题主要考查了整式的混合运算以及负指数幂的性质、零指数幂的性质,正确掌握相关运算法则是解题关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
12.1+0.2%等于( )
| A. | 1.2% | B. | 1.02% | C. | 1.002% | D. | 100.2% |
9.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.下表是某周的生产情况(增产为正,减产为负):
(1)根据记录可知,前三天共生产了599辆自行车;
(2)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣5元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣5元,那么该厂工人这一周的工资总额是多少?
16. 如图,?ABCD中,∠C=120°,AB=AE=5,AE与BD交于点F,AF=2EF,则BC的长为( )
如图,?ABCD中,∠C=120°,AB=AE=5,AE与BD交于点F,AF=2EF,则BC的长为( )
 如图,?ABCD中,∠C=120°,AB=AE=5,AE与BD交于点F,AF=2EF,则BC的长为( )
如图,?ABCD中,∠C=120°,AB=AE=5,AE与BD交于点F,AF=2EF,则BC的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
(1)上表中,自变量是物体的质量,因变量是弹簧的长度.
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
| 所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 弹簧的长度/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
10.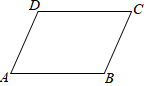 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )| A. | AB=DC | B. | AD∥BC | C. | ∠A+∠B=180° | D. | ∠A+∠D=180° |
11.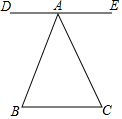 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )
 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |