题目内容
已知⊙O是△ABC的外接圆,且BC=
,⊙O的半径为1,求∠A的度数.
| 2 |
考点:圆周角定理,等腰直角三角形
专题:
分析:分为两种情况:①当A在优弧BC上时,连接OB、OC,过O作OD⊥BC于D,根据垂径定理求出BD=DC=
BC=
,在Rt△ODC中解直角三角形求出∠DOC=45°,求出∠BOC=90°,根据圆周角定理得出∠A=
∠BOC即可;②根据圆内接四边形性质求出即可.
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答: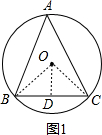
解:分为两种情况:①如图1,当A在优弧BC上时,连接OB、OC,过O作OD⊥BC于D,
∵BC=
,
∴BD=DC=
BC=
,
∴在Rt△ODC中,sin∠DOC=
=
=
,
∴∠DOC=45°,
同理∠BOD=45°,
∴∠BOC=90°,
由圆周角定理得:∠A=
∠BOC=45°;
②如图2,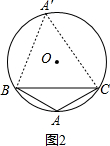
由①知:∠A′=45°,
∵A′、B、A、C四点共圆,
∴∠A′+∠A=180°,
∴∠A=135°,
即∠A的度数为45°或135°.

解:分为两种情况:①如图1,当A在优弧BC上时,连接OB、OC,过O作OD⊥BC于D,
∵BC=
| 2 |
∴BD=DC=
| 1 |
| 2 |
| ||
| 2 |
∴在Rt△ODC中,sin∠DOC=
| CD |
| OC |
| ||||
| 1 |
| ||
| 2 |
∴∠DOC=45°,
同理∠BOD=45°,
∴∠BOC=90°,
由圆周角定理得:∠A=
| 1 |
| 2 |
②如图2,

由①知:∠A′=45°,
∵A′、B、A、C四点共圆,
∴∠A′+∠A=180°,
∴∠A=135°,
即∠A的度数为45°或135°.
点评:本题考查了圆周角定理,垂径定理,解直角三角形,圆内接四边形性质的应用,注意:要进行分类讨论,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=
如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=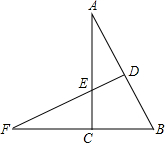 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,ED所在直线是线段AB的垂直平分线,若直线ED分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,ED所在直线是线段AB的垂直平分线,若直线ED分别交AB、AC及BC的延长线于点D、E、F,连接BE,求证:EF=2DE.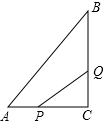 在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动.
在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动. 如图,直角梯形OABC,CB∥OA,OC=4
如图,直角梯形OABC,CB∥OA,OC=4