题目内容
3.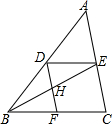 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{EC}$ | C. | $\frac{DE}{BF}$=$\frac{AE}{EC}$ | D. | $\frac{EH}{HB}$=$\frac{AE}{EC}$ |
分析 先求出四边形DFCE是平行四边形,求出DE=CF,再根据平行线分线段定理和相似三角形的性质逐个判断即可.
解答 解:A、∵DE∥BC,
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$,故本选项错误;
B、∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$≠$\frac{AE}{EC}$,故本选项正确;
C、∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=FC,
∵DE∥BC,DF∥AC,
∴$\frac{FC}{BF}$=$\frac{AD}{BD}$,$\frac{AD}{BD}$=$\frac{AE}{EC}$,
∴$\frac{DE}{BF}$=$\frac{AE}{EC}$,故本选项错误;
D、∵DE∥BC,
∴△DEH∞△FBH,
∴$\frac{EH}{HB}$=$\frac{DE}{BF}$,
∵$\frac{DE}{BF}$=$\frac{AE}{EC}$,
∴$\frac{EH}{HB}$=$\frac{AE}{EC}$,故本选项错误;
故选B.
点评 本题考查了相似三角形的性质和判定,平行线分线段成比例定理的应用,能灵活运用定理得出比例式是解此题的关键.

练习册系列答案
相关题目
8.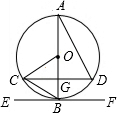 如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )
 如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )| A. | EF∥CD | B. | △COB是等边三角形 | ||
| C. | CG=DG | D. | $\widehat{BC}$的长为$\frac{3}{2}$π |
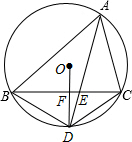 如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )
如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( ) 如图是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )
如图是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )




 如图,O是直线AD上一点,射线OC、OE分别是∠AOB,∠BOD的平分线,若∠DOE=60°,则∠BOC=30度.
如图,O是直线AD上一点,射线OC、OE分别是∠AOB,∠BOD的平分线,若∠DOE=60°,则∠BOC=30度.