题目内容
13.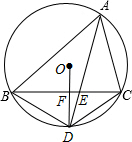 如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )
如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )①∠BFO=90°;
②$\widehat{BD}$=$\widehat{DC}$=$\frac{1}{2}$$\widehat{BDC}$;
③BF=FC=$\frac{1}{2}$BC;
④BE=EC=$\frac{1}{2}$BC;
⑤∠BAD=∠DAC=$\frac{1}{2}$∠BAC.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据垂径定理求出OD⊥BC,得出①正确;由圆周角定理得出$\widehat{BD}$=$\widehat{CD}$,②正确;由等腰三角形的性质得出③正确,④错误;由角平分线得出⑤正确;即可得出结论.
解答 解:①∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴$\widehat{BD}$=$\widehat{CD}$,
∵OD为半径,
∴DO⊥BC,
∴∠BFO=90°,
故①正确;
②∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴$\widehat{BD}$=$\widehat{CD}$,
∴$\widehat{BD}$=$\widehat{DC}$=$\frac{1}{2}$$\widehat{BDC}$,
故②正确;
③连接OB、OC,如图所示:
由①知DO⊥BC,
∵OB=OC,
∴BF=FC=$\frac{1}{2}$BC,
故③正确;
④∵BF=FC=$\frac{1}{2}$BC
∴BE=EC=$\frac{1}{2}$BC错误,
故④不正确;
⑤∵AD平分∠BAC,
∴∠BAD=∠DAC,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC,
故⑤正确;
综上所述:正确的有①②③⑤;
故答案为:B.
点评 本题考查了垂径定理、圆周角定理、等腰三角形的性质等知识;熟练掌握垂径定理和圆周角定理是解决问题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.为了了解开展“尊敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用的时间,得到一组数据,并绘制制成下表,请根据下表完成下列各题:
(1)填写表中未完成的部分;
(2)这组数据的中位数是2.5小时,众数是3小时;
(3)该班学生每周做家务的平均时间是多少小时(写出计算的过程)
| 每周做家务的时间(小时) | 0 | 1 | 2 | 3 | 4 | 合计 |
| 人数 | 2 | 6 | 17 | 20 | 5 | 50 |
(2)这组数据的中位数是2.5小时,众数是3小时;
(3)该班学生每周做家务的平均时间是多少小时(写出计算的过程)
8. 如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
 如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )| A. | 20° | B. | 70° | C. | 100° | D. | 110° |
18.一个盒子中放着三种颜色的球,每个球除颜色外都相同,红球x个,白球7个,黑球y个,如果从中任取一个球,取得的白球的概率比取得非白球的概率大,那么x与y的关系是( )
| A. | x+y=7 | B. | x+y>7 | C. | y-x>7 | D. | x+y<7 |
2.雾霾天气影响着我国北方中东部地区,给人们的健康带来严重的危害,为了让人们更好地了解雾霾,张超通过显微镜,将空气中细小的霾颗粒放大1000倍,发现这些霾颗粒平均值约为15微米,其中15微米(1米=1000000微米)用科学记数法可表示为( )
| A. | 1.5×105米 | B. | 0.15×10-1米 | C. | 1.5×10-5米 | D. | 15×10-6米 |
3.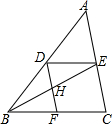 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{EC}$ | C. | $\frac{DE}{BF}$=$\frac{AE}{EC}$ | D. | $\frac{EH}{HB}$=$\frac{AE}{EC}$ |

 如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).
如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).