题目内容
8.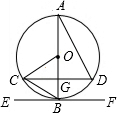 如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )| A. | EF∥CD | B. | △COB是等边三角形 | ||
| C. | CG=DG | D. | $\widehat{BC}$的长为$\frac{3}{2}$π |
分析 根据切线的性质定理和垂径定理判断A;根据等边三角形的判定定理判断B;根据垂径定理判断C;利用弧长公式计算出$\widehat{BC}$的长判断D.
解答 解:∵AB为⊙O的直径,EF切⊙O于点B,
∴AB⊥EF,又AB⊥CD,
∴EF∥CD,A正确;
∵AB⊥弦CD,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠COB=2∠A=60°,又OC=OD,
∴△COB是等边三角形,B正确;
∵AB⊥弦CD,
∴CG=DG,C正确;
$\widehat{BC}$的长为:$\frac{60×π×3}{180}$=π,D错误,
故选:D.
点评 本题考查的是垂径定理、弧长的计算、切线的性质,掌握弧长的计算公式l=$\frac{nπr}{180}$、切线的性质定理以及垂径定理是解题的关键.

练习册系列答案
相关题目
18.一个盒子中放着三种颜色的球,每个球除颜色外都相同,红球x个,白球7个,黑球y个,如果从中任取一个球,取得的白球的概率比取得非白球的概率大,那么x与y的关系是( )
| A. | x+y=7 | B. | x+y>7 | C. | y-x>7 | D. | x+y<7 |
16.下列几何体的三视图相同的是( )
| A. |  圆柱 | B. |  球 | C. |  圆锥 | D. |  长方体 |
3.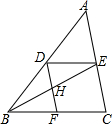 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{EC}$ | C. | $\frac{DE}{BF}$=$\frac{AE}{EC}$ | D. | $\frac{EH}{HB}$=$\frac{AE}{EC}$ |
13.五名同学参加演讲比赛,以抽签的方式决定每个人的出场顺序.把背面完全相同,正面写有1、2、3、4、5的五张卡片洗均后正面向下放在桌子上,小军从中随机抽取一张,下列事件是随机事件的是( )
| A. | 抽到的数字是0 | B. | 抽到的数字是7 | C. | 抽到的数字大于5 | D. | 抽到的数字是1 |
20. 如图所示三棱柱的主视图是( )
如图所示三棱柱的主视图是( )
 如图所示三棱柱的主视图是( )
如图所示三棱柱的主视图是( )| A. |  | B. |  | C. |  | D. |  |
17.-$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | -3 | C. | 3 | D. | -$\frac{1}{3}$ |
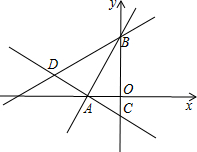 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根