题目内容
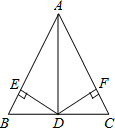 如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,(1)要得到DE=DF,点D应满足什么条件?
(2)在(1)的条件下,试探究直线AD上任意一点P所具有的特征,并说明理由.
考点:角平分线的性质,等腰三角形的性质
专题:
分析:(1)根据到角的两边距离相等的点在角的平分线上判断出AD平分∠BAC,再根据等腰三角形三线合一的性质解答;
(2)根据等腰三角形三线合一的性质判断出AD垂直平分BC,再根据线段垂直平分线上的点到两端点的距离相等解答.
(2)根据等腰三角形三线合一的性质判断出AD垂直平分BC,再根据线段垂直平分线上的点到两端点的距离相等解答.
解答:解:(1)∵DE⊥AB,DF⊥AC,DE=DF,
∴AD平分∠BAC,
∵AB=AC,
∴BD=CD,
故点D是BC的中点;
(2)∵AB=AC,点D是BC的中点,
∴AD垂直平分BC,
∴直线AD上任意一点P到B、C两点的距离相等.
∴AD平分∠BAC,
∵AB=AC,
∴BD=CD,
故点D是BC的中点;
(2)∵AB=AC,点D是BC的中点,
∴AD垂直平分BC,
∴直线AD上任意一点P到B、C两点的距离相等.
点评:本题考查了到角的两边距离相等的点在角的平分线上,等腰三角形三线合一的性质,线段垂直平分线上的点到两端点的距离相等的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
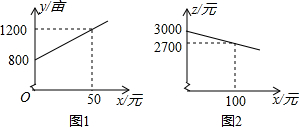 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. 如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.
如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.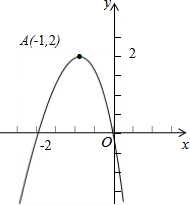 (1)请写出图中所示的二次函数图象的解析式;
(1)请写出图中所示的二次函数图象的解析式;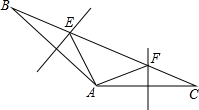 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.