题目内容
有一根长70厘米的木棒， （填“能”或“不能”）放进长、宽、高分别为50厘米、40厘米、30厘米的空木箱中．
考点：勾股定理的应用
专题：
分析：在长方体的木箱中，一角的顶点与斜对的不共面的顶点的距离最大，根据木箱的长，宽，高可求出最大距离，然后和木棒的长度进行比较．
解答：解：可设放入长方体盒子中的最大长度是xcm，
根据题意，得x2=502+402+302=5000，
702=4900，
因为4900＜5000，
所以能放进去．
故答案为：能．
根据题意，得x2=502+402+302=5000，
702=4900，
因为4900＜5000，
所以能放进去．
故答案为：能．
点评：本题考查了勾股定理的应用，解题的关键是求出木箱内木棒的最大长度．
练习册系列答案
相关题目
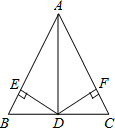如图，在△ABC中，AB=AC，D为BC上一点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，
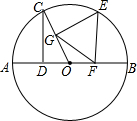如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB于D，且∠COD=60°，E为弧BC上一动点（不与点B、C重合），过E分别作于EF⊥AB于F，EG⊥OC于G．