如图.下列条件不能判定△ABC与△ADE相似的是( )A．$\frac{AE}{AC}$=$\frac{DE}{BC}$B．∠B=∠ADEC．$\frac{AE}{AD}$=$\frac{AC}{AB}$D．∠C=∠AED 题目和参考答案——青夏教育精英家教网—

题目内容

14．

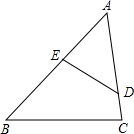如图，下列条件不能判定△ABC与△ADE相似的是（　　）

A．

$\frac{AE}{AC}$=$\frac{DE}{BC}$

B．

∠B=∠ADE

C．

$\frac{AE}{AD}$=$\frac{AC}{AB}$

D．

∠C=∠AED

分析根据相似三角形的判定即可判断．

解答解：（B）∵∠A=∠A，
∠B=∠ADE，
∴△ABC∽△ADE，故B可以判断，
（C）∵$\frac{AE}{AD}=\frac{AC}{AB}$
∠A=∠A
∴△ABC∽△ADE，故C可以判断，
（D）∵∠A=∠A，
∠C=∠AED，
∴△ABC∽△ADE，故D可以判断，
故选（A）

点评本题考查相似三角形的判定，解题的关键是熟练运用相似三角形的判定，本题属于基础题型．

练习册系列答案

初中毕业生学业水平巩固与提高系列答案

安童教育中考模拟试卷系列答案

考必胜小学毕业升学考试试卷精选系列答案

5．阅读下列解题过程：$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{1×（\sqrt{5}-\sqrt{4}）}{（\sqrt{5}+\sqrt{4}）（\sqrt{5}-\sqrt{4}）}$=$\frac{\sqrt{5}-\sqrt{4}}{（\sqrt{5}）^{2}-（\sqrt{4}）^{2}}$=$\sqrt{5}$-$\sqrt{4}$=$\sqrt{5}$-2；
$\frac{2}{\sqrt{6}-\sqrt{5}}$=$\frac{2×（\sqrt{6}+\sqrt{5}）}{（\sqrt{6}-\sqrt{5}）（\sqrt{6}+\sqrt{5}）}$=$\frac{2\sqrt{6}+2\sqrt{5}}{（\sqrt{6}）^{2}-（\sqrt{5}）^{2}}$=2$\sqrt{6}$+2$\sqrt{5}$；
请解答下列问题：
（1）观察上面解题过程，计算$\frac{3}{\sqrt{10}-\sqrt{7}}$；
（2）请直接写出$\frac{1}{\sqrt{n}+\sqrt{n-1}}$的结果．（n≥1）
（3）利用上面的解法，请化简：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{98}+\sqrt{99}}$+$\frac{1}{\sqrt{99}+\sqrt{100}}$．

$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$

B．

$\sqrt{3}$×（$\sqrt{8}$-$\sqrt{2}$）=$\sqrt{3}$×$\sqrt{6}$=$\sqrt{18}$

C．

$\sqrt{9}$=±3

D．

|$\sqrt{5}$-$\sqrt{7}$|=$\sqrt{7}$-$\sqrt{5}$

19．在代数式$\frac{ab}{3}$，$-\frac{2}{3}$abc，-5，x-y，$\frac{2}{x}$，π中，单项式有（　　）

6．把数-2，1.5，-（-4），-3$\frac{1}{2}$，（-1）⁴，-|+0.5|在数轴上表示出来，然后用“＜”把它们连接起来．

3．

如图，已知△ABC≌△ADE，∠C=79°，DE⊥AB，则∠D的度数为68°．

4．已知点A（a，4），B（-2，b）．
（1）若AB∥x轴，求b的值；
（2）若A、B两点在第二象限的角平分线上，求a、b的值．

试题分类