题目内容
20．
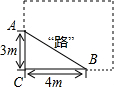如图，某学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”AB，爱心小组想在A处树立一个标牌“少走■米，踏之何刃？”请你计算后帮她们在标牌的■填上适当的数字为2米．
分析 利用勾股定理求出AB的长即可解决问题．
解答 解：在Rt△ABC中，∵AC=3m，BC=4m，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5m，
3+4-5=2，
故答案为2米．
点评 本题考查勾股定理的应用，解题的关键是理解题意，灵活运用勾股定理解决实际问题，属于中考常考题型．
练习册系列答案
相关题目
11．
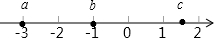已知有理数a，b，c在数轴上的位置如图所示，则下列说法中不正确的是（ ）
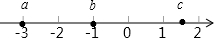已知有理数a，b，c在数轴上的位置如图所示，则下列说法中不正确的是（ ）| A． | a=-3 | B． | b=-1 | ||
| C． | a的相反数大于b的相反数 | D． | c可能等于2.5 |
有理数m，n在数轴上的位置如图所示，化简$\sqrt{{m}^{2}}$-$\sqrt{{n}^{2}}$-$\sqrt{（m-n）^{2}}$=-2n．
15．若14x6y2与-31x3my2的和是单项式，则式子12m-24的值是（ ）
| A． | -3 | B． | -5 | C． | -4 | D． | 0 |
如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，求∠CDF的度数．
9．下列运算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | $\sqrt{3}$×（$\sqrt{8}$-$\sqrt{2}$）=$\sqrt{3}$×$\sqrt{6}$=$\sqrt{18}$ | C． | $\sqrt{9}$=±3 | D． | |$\sqrt{5}$-$\sqrt{7}$|=$\sqrt{7}$-$\sqrt{5}$ |
10．下列给出的数轴中正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |