题目内容
10．若a＞1，则1+$\frac{\sqrt{（1-a）^{2}}}{a-1}$的值是（ ）| A． | 1 | B． | 2 | C． | 0 | D． | -1 |
分析 $\sqrt{{a}^{2}}$=|a|可得$\sqrt{（1-a）^{2}}$=|1-a|，再根据绝对值的性质去绝对值符号，再化简计算即可．
解答 解：1+$\frac{\sqrt{（1-a）^{2}}}{a-1}$=1+$\frac{|1-a|}{a-1}$=1+$\frac{a-1}{a-1}$=1+1=2，
故选：B．
点评 此题主要考查了二次根式的性质和化简，关键是掌握$\sqrt{{a}^{2}}$=|a|．
练习册系列答案
相关题目
12．下列计算正确的是（ ）
| A． | （-x3）2=x5 | B． | （-3x2）2=6x4 | C． | （-x）-2=$\frac{1}{{x}^{2}}$ | D． | x8÷x4=x2 |
如图，AE∥BF，AC平分∠BAE，交BF于C．
如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC=3：5，AB=8．
5．在△ABC中，∠C=90°，tanA=1，则∠B的度数是（ ）
| A． | 75° | B． | 60° | C． | 45° | D． | 30° |
15．下列说法中正确的是（ ）
| A． | 随机抛掷一枚均匀的硬币，落地后反面一定朝上 | |
| B． | 从1、3、5、7、9中随机取一个数，取得的数不可能是偶数 | |
| C． | “彩票的中奖机会是1%”表示买100张彩票一定会中奖 | |
| D． | “明天降雨的概率是85%”表示明天有85%的时间降雨 |
2．已知$\sqrt{4.4}$=m，$\sqrt{44}$=n，则$\sqrt{0.044}$=（ ）
| A． | 10n | B． | $\frac{n}{10}$ | C． | 10m | D． | $\frac{m}{10}$ |
19．某校七（7）班50名学生的校服尺码经统计如下：
求这50名学生的校服尺码的平均数．
| 尺码（单位：cm） | 人数 |
| 140≤x＜150 | 7 |
| 150≤x＜160 | 30 |
| 160≤x＜170 | 10 |
| 170≤x＜180 | 3 |
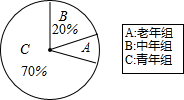2015年12月，某市总工会组织该市各单位参加“迎新春长跑活动”，组委会将男运动员分成三组：老年组、中年组和青年组，根据报名情况，制作了如图所示的人数扇形统计图，已知青年组共有210人，则老年组共有30人．