题目内容
15. 如图所示,△A′B′C′是△ABC平移后得到的,△ABC内任意一点M(x0,y0)平移后对应点M(x0-5,y0-3)
如图所示,△A′B′C′是△ABC平移后得到的,△ABC内任意一点M(x0,y0)平移后对应点M(x0-5,y0-3)(1)试述△ABC是经过怎样平移后变为△A′B′C′的?
(2)求A′B′C′的坐标;
(3)求S△A′B′C′的值.
分析 (1)根据M点的坐标变化即可得出结论;
(2)根据M(x0,y0)平移后对应点M(x0-5,y0-3)得到坐标的变化规律,即可求出A′B′C′的坐标;
(3)根据S△A′B′C′=S△ABC=S矩形BGDE-S△BGC-S△ADC-S△ABE=进行解答.
解答  解:(1)将ABC向左平移5个单位,向下平移3各单位即可得到△A′B′C′;
解:(1)将ABC向左平移5个单位,向下平移3各单位即可得到△A′B′C′;
(2)A(3,6),B(1,2),C(6,4)的横坐标-5,纵坐标-3即可得A′(-2,3);B′(-4,-1);C′(1,1).
(3)如图,S△A′B′C′=S△ABC=S矩形BGDE-S△BGC-S△ADC-S△ABE=5×4-$\frac{1}{2}$×5×2-$\frac{1}{2}$×3×2-$\frac{1}{2}$×2×5=7.
点评 本题考查了作图--平移变换,根据坐标变化得出图形变化规律是解题的关键.

练习册系列答案
相关题目
7. 菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
 菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )| A. | (-1,$\sqrt{3}$) | B. | (-3,$\sqrt{3}$) | C. | (-3,$\sqrt{2}$) | D. | (3,$\sqrt{3}$) |
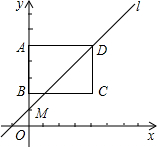 如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
 如图,菱形ABCD的周长为12cm,相邻两角的度数之比为5:1,求菱形对边AB与CD之间的距离.
如图,菱形ABCD的周长为12cm,相邻两角的度数之比为5:1,求菱形对边AB与CD之间的距离.