题目内容
20. 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
分析 (1)由已知条件可得RT△CDF中∠C=30°,即可知DF=$\frac{1}{2}$CD=AE=2t;
(2)由(1)知DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;
(3)四边形BEDF不为正方形,若该四边形是正方形即∠EDF=90°,即DE∥AB,此时AD=2AE=4t,根据AD+CD=AC求得t的值,继而可得DF≠BF,可得答案.
解答 解:(1)∵RT△ABC中,∠B=90°,∠A=60°,
∴∠C=90°-∠A=30°.
又∵在RT△CDF中,∠C=30°,CD=4t
∴DF=$\frac{1}{2}$CD=2t,
∴DF=AE;
(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60-4t=2t,解得:t=10,
即当t=10时,四边形AEFD是菱形;
(3)四边形BEDF不能为正方形,理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t=$\frac{15}{2}$时,∠EDF=90°
但BF≠DF,
∴四边形BEDF不可能为正方形.
点评 本题主要考查直角三角形的性质、平行四边形的判定、菱形的性质、正方形的性质等知识点,熟练掌握平行四边形、菱形、正方形的判定是解题的关键.

练习册系列答案
相关题目
10. 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
11.借助计算器可求得$\sqrt{{4^2}+{3^2}}=5,\sqrt{{{44}^2}+{{33}^2}}=55,\sqrt{{{444}^2}+{{333}^2}}$=555,…,仔细观察上面几道题的计算结果,试猜想$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=( )
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
15. 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )
 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )| A. |  | B. |  | C. |  | D. |  |
5.如果单项式2anb2c是六次单项式,那么n=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
9. 如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
 如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )| A. | 10° | B. | 15° | C. | 40° | D. | 50° |
10.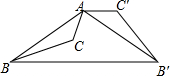 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
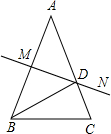 如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.
如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.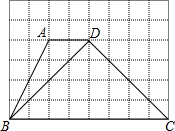 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,连接BD.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,连接BD.