题目内容
4．解答题（1）已知：a=-2，b=20，c=-3，且a-（-b）+c-d=10，求d的值．
（2）已知|a+2|+|b+3|=0，求a+b的值．
分析 （1）根据有理数的加减混合运算法则计算即可；
（2）根据非负数的性质列出算式，求出a、b的值，计算即可．
解答 解：（1）∵a-（-b）+c-d=10，
∴d=10-a-b-c=10+2-20+3=-5；
（2）由题意得，a+2=0，b+3=0，
解得，a=-2，b=-3，
则a+b=-5．
点评 本题考查的是非负数的性质和有理数的计算，掌握几个非负数相加和为0时，则其中的每一项都必须等于0是解题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
14．顺次连接矩形四边中点所组成的图形是（ ）
| A． | 菱形 | B． | 矩形 | C． | 平行四边形 | D． | 无法确定 |
12．
如图，直线AB∥CD，直线EF与直线AB相交于点M，MN平分∠AME，若∠1=50°，则∠2的度数为（ ）
如图，直线AB∥CD，直线EF与直线AB相交于点M，MN平分∠AME，若∠1=50°，则∠2的度数为（ ）| A． | 50° | B． | 80° | C． | 85° | D． | 100° |
如图，在平行四边形ABCD中，AC与BD交于点O，点E是BC边上的中点，AB=6，则OE=3．
9．小明在某商店购买商品A、B共两次，这两次购买商品A、B的数量和费用如表：
若小明需要购买3个商品A和2个商品B，则她要花费（ ）
| 购买商品A的数量（个） | 购买商品B的数量（个） | 购买总费用（元） | |
| 第一次购物 | 4 | 3 | 93 |
| 第二次购物 | 6 | 6 | 162 |
| A． | 64元 | B． | 65元 | C． | 66元 | D． | 67元 |
16．
如图，在?ABCD中，对角线AC、BD相交于点O，且OA=OB，若AD=4，∠AOD=60°，则AB的长为（ ）
如图，在?ABCD中，对角线AC、BD相交于点O，且OA=OB，若AD=4，∠AOD=60°，则AB的长为（ ）| A． | 4$\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 8 | D． | 8$\sqrt{3}$ |
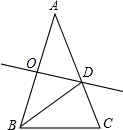如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，以下结论：
完成下面证明：如图，B是射线AD上一点，∠DAE=∠CAE，∠DAC=∠C=∠CBE