题目内容
6.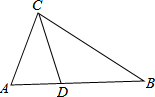 如图,在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC.
如图,在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC.
分析 在BC上截取CE=AC,连接DE,利用已知条件求证△ACD≌△ECD,然后可得AD=DE,∠A=∠CED,再利用三角形外角的性质求证DE=EB,然后问题可解.
解答 证明:在BC上截取AC=CE,连接DE.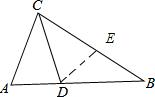
∵∠ACB的平分线CD交AB边于点D,
∴∠ACD=∠DCE,
在△ACD与△ECD中,
$\left\{\begin{array}{l}{AC=CE}\\{∠ACD=∠DCE}\\{CD=CD}\end{array}\right.$,
∴△ACD≌△ECD(SAS),
∴AD=DE,∠A=∠CED,
∵∠A=2∠B,∠CED=∠B+∠EDC,
∴∠CED=2∠B,
∴∠B=∠EDC,
∴DE=BE,
∴AD=EB,
∴AC+AD=BC.
点评 此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,证明此题的关键是在BC上截取AC=CE,连接DE,利用已知条件求证△ACD≌△DCE,此题难易程度适中,适合学生的训练.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
16.下列各组式子中,同类项有( )
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
14.下列命题中,是真命题的是( )
| A. | 圆的半径都相等 | |
| B. | 如果两条弧的长都是8cm,那么这两条弧是等弧 | |
| C. | 圆心是直径的中点 | |
| D. | 到一个圆的圆心距离相等的点不一定在这个圆上 |
 如图,过点P(0,-2)的直线l与抛物线y=x2只有一个公共点M,求点M的坐标.
如图,过点P(0,-2)的直线l与抛物线y=x2只有一个公共点M,求点M的坐标.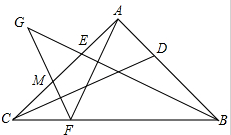 如图,等腰三角形ABC中,∠BAC=90°,D,E分别为AB,AC边上的点.AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD,交BE于点G,交AC于点M.
如图,等腰三角形ABC中,∠BAC=90°,D,E分别为AB,AC边上的点.AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD,交BE于点G,交AC于点M.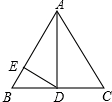 如图,在等边△ABC中,AD是中线,DE⊥AB,垂足为E,若BC=4cm.则DE的长$\sqrt{3}$cm.
如图,在等边△ABC中,AD是中线,DE⊥AB,垂足为E,若BC=4cm.则DE的长$\sqrt{3}$cm.