题目内容
15．正n边形的中心角与它的一个内角的关系是互补．分析 根据正多边形的中心角的定义可得到正多边形的中心角等于正多边形的一个外角，然后利用正多边形的一个外角与该正多边形相邻的一个内角互补得到正多边形的中心角与该正多边形一个内角互补．
解答 解：∵正n边形的中心角为$\frac{360°}{n}$，正n边形的一个外角等于$\frac{360°}{n}$，
所以正n边形的中心角等于正n边形的一个外角，
而正n边形的一个外角与该正n边形相邻的一个内角的互补，
所以正n边形的中心角与该正n边形一个内角互补，
故答案为：互补．
点评 本题考查了正多边形与圆：把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆，掌握正多边形的中心角为$\frac{360°}{n}$，正多边形的一个外角等于$\frac{360°}{n}$是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
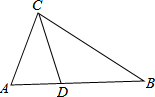如图，在△ABC中，∠BAC=2∠B，CD平分∠ACB交AB于D，求证：AC+AD=BC．
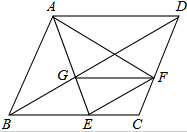已知，如图，在菱形ABCD中，点E、F分别在边BC、CD，∠BAF=∠DAE，AE与BD交于点G．