题目内容
9.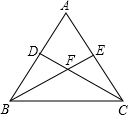 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
分析 (1)证得△ABE≌△ACD后利用全等三角形的对应角相等即可证得结论;
(2)利用垂直平分线段的性质即可证得结论.
解答 解:(1)∠ABE=∠ACD;
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD,
∴∠ABE=∠ACD;
(2)∵AB=AC,
∴∠ABC=∠ACB,
由(1)可知∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴FB=FC,
∵AB=AC,
∴点A、F均在线段BC的垂直平分线上,
即直线AF垂直平分线段BC.
点评 本题考查了等腰三角形的性质及垂直平分线段的性质的知识,解题的关键是能够从题目中整理出全等三角形,难度不大.

练习册系列答案
相关题目
17.2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
14.下列运算正确的是( )
| A. | 3x2+4x2=7x4 | B. | 2x3•3x3=6x3 | C. | a÷a-2=a3 | D. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 |
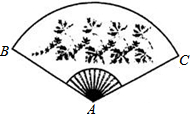 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)