题目内容
10. 如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.
如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.
分析 连接OD,DE,由PD是⊙O的切线,得到OD⊥PD,根据垂径定理得到OC⊥OP,于是得到∠DAC=∠DPE,∠DPF=∠DBF,推出P,A,E,D,四点共圆,P,B,F,D四点共圆,根据圆周角定理得到∠DEC=∠DPA,∠DFC=∠DPA,等量代换得到∠DEC=∠DFC,推出D,E,F,C四点共圆,根据圆周角定理即刻得到结论.
解答 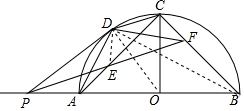 证明:连接OD,DE,
证明:连接OD,DE,
∵PD是⊙O的切线,
∴OD⊥PD,
∵C为半圆弧O的中点,
∴OC⊥OP,
∴∠DPB+∠DOP=∠DOP+∠DOC,
∴∠DPB=∠DOC=2∠DAC=2∠DBC=2∠DPF,
即∠DAC=∠DPE,∠DPF=∠DBF,
∴P,A,E,D,四点共圆,P,B,F,D四点共圆,
∴∠DEC=∠DPA,∠DFC=∠DPA,
∴∠DEC=∠DFC,
∴D,E,F,C四点共圆,
∴∠CDF=∠CEF=∠PEA=∠PDA.
即:∠PDA=∠CDF.
点评 本题考查了切线的性质,垂径定理,圆周角定理,四点共圆,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
19.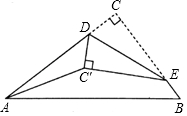 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )| A. | 不存在 | B. | 等于1cm | C. | 等于2 cm | D. | 等于2.5 cm |
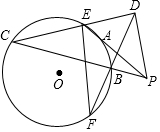 PA为⊙O的切线,PBC是⊙O的割线,PD=PA,连接CD,BD分别交⊙O于E,F,求证:EF∥PD.
PA为⊙O的切线,PBC是⊙O的割线,PD=PA,连接CD,BD分别交⊙O于E,F,求证:EF∥PD. 如图,AB=2BC,D为AC的中点,DC=3cm,求AB的长.
如图,AB=2BC,D为AC的中点,DC=3cm,求AB的长.