题目内容
15.若x4+ax2-bx+2能被x2+3x+2整除,则a+b=3.分析 首先把x2+3x+2因式分解,利用整除的性质可知x2+3x+2每一个因式可整除x4+ax2-bx+2,每一个因式为0的x的值,同样使x4+ax2-bx+2为0,由此联立方程解答即可.
解答 解:由于x2+3x+2=(x+1)(x+2),
假如f(x)能被x2+3x+2整除,则(x+1)和(x+2)必是f(x)的因式,
因此,当x=-1时,f(-1)=0,即1+a+b+2=0,①
当x=-2时,f(-2)=0,即16+4a+2b+2=0,②
由①,②联立,则有$\left\{\begin{array}{l}{1+a+b+2=0}\\{16+4a+2b+2=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-6}\\{b=3}\end{array}\right.$,
∴a+b=-6+3=3,
故答案为3.
点评 本题考查了整式的除法,掌握利用整除的性质建立二元一次方程组解答问题是解题的主要思想,也是解题的关键.

练习册系列答案
相关题目
4.某市2015年国内生产总值(GDP)比2014年增长了12%,预计2016年比2015年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=(1+x%)2 |
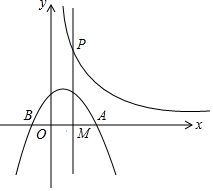 如图,抛物线C:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,若OA•MP=12.
如图,抛物线C:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,若OA•MP=12. 如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.
如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.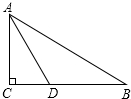 如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D点到直线AB的距离是5cm.
如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D点到直线AB的距离是5cm.
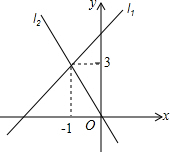 直线l1:y=k1x+b与直线l2:y=k2X在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}y={k_1}x+b\\ y={k_2}x\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$.
直线l1:y=k1x+b与直线l2:y=k2X在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}y={k_1}x+b\\ y={k_2}x\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$.