题目内容
20.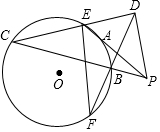 PA为⊙O的切线,PBC是⊙O的割线,PD=PA,连接CD,BD分别交⊙O于E,F,求证:EF∥PD.
PA为⊙O的切线,PBC是⊙O的割线,PD=PA,连接CD,BD分别交⊙O于E,F,求证:EF∥PD.
分析 根据切割线定理得到PA2=PB•PC,等量代换得到PD2=PB•PC,推出△PBD∽△PDC,根据相似三角形的性质得到∠PDB=∠C,由圆周角定理得到∠C=∠F,等量代换得到∠F=∠PDB,根据平行线的判定即刻得到结论.
解答 证明:∵PA为⊙O的切线,PBC是⊙O的割线,
∴PA2=PB•PC,
∵PD=PA,
∴PD2=PB•PC,
∴$\frac{PD}{PB}$=$\frac{PC}{PD}$,
∵∠DPC=∠BPD,
∴△PBD∽△PDC,
∴∠PDB=∠C,
∵∠C=∠F,
∴∠F=∠PDB,
∴EF∥PD.
点评 本题考查了切线的性质,切割线定理,相似三角形的判定和性质,平行线的判定,熟记掌握切割线定理是解题的关键.

练习册系列答案
相关题目
10.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程y(千米)与行驶时间x(小时)之间的函数关系式是( )
| A. | y=80x-100 | B. | y=-80x-100 | C. | y=80x+100 | D. | y=-80x+100 |
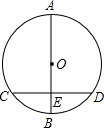 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.
 如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.
如图,C为半圆弧O的中点,点P为直径BA延长线上一点,过点P作半圆的切线PD,D为切点,∠DPB的平分线分别交AC,BC于点E,F; 证明:∠PDA=∠CDF.