题目内容
16.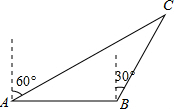 如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
分析 过C作CD⊥AB延长线于点D,根据已知分别在Rt△CBD中,在Rt△ADC中用式子表示CD,从而求得CD的长,再与11作比较,若大于11则没有危险,否则有危险.
解答  解:如图,过C作CD⊥AB延长线于点D,易求AB=18×$\frac{40}{60}$=12(海里).
解:如图,过C作CD⊥AB延长线于点D,易求AB=18×$\frac{40}{60}$=12(海里).
在Rt△CBD中,∠CBD=60°,
在Rt△ADC中,∠CAB=30°,
∵∠CBD=∠CAB+∠ACB=60°
∴∠ACB=∠CAB=30°,
∴BC=AB=12海里,
则CD=BC•sin∠CBD=BC•sin60°=$\frac{\sqrt{3}}{2}$BC,
∴CD=6$\sqrt{3}$(海里)
∵6$\sqrt{3}$<11,
∴继续向东航行,有触礁的危险.
点评 此题主要考查了方向角的应用,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
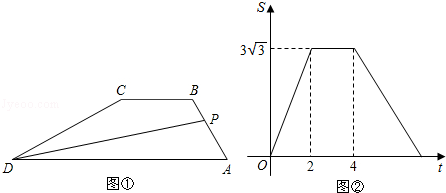
6.如图①,在四边形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向向点D移动,已知△PAD的面积S(单位:cm2)与点P移动的时间t(单位:s)的函数如图②所示,则点P从开始移动到停止共用时( )

| A. | 8秒 | B. | (4+$2\sqrt{3}$)秒 | C. | (4+3$\sqrt{3}$)秒 | D. | (4+$\sqrt{3}$)秒 |
 如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长.
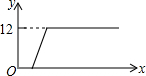
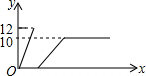
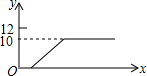
如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长. 如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )
如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )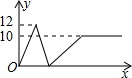
 如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.
如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.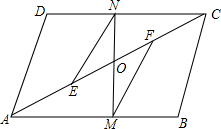 如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分.
如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分.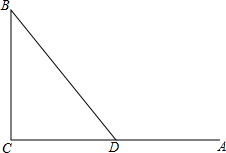 如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).
如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD). 如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C
如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C