题目内容
5．设变量x满足x2+bx≤-x（b＜-1）．并且x2+bx的最小值是-$\frac{1}{2}$，求b的值．分析 利用配方法对（x2+bx）变形得到x2+bx=（x+$\frac{b}{2}$）2-$\frac{{b}^{2}}{4}$≥-$\frac{{b}^{2}}{4}$，结合已知条件可以求得b的值．
解答 解：∵x2+bx=（x+$\frac{b}{2}$）2-$\frac{{b}^{2}}{4}$≥-$\frac{{b}^{2}}{4}$，x2+bx的最小值是-$\frac{1}{2}$，
∴-$\frac{{b}^{2}}{4}$=-$\frac{1}{2}$
解得b=±$\sqrt{2}$．
∵b＜-1，
∴b=-$\sqrt{2}$．
点评 本题考查了配方法的应用．解题时，注意b的取值范围是b＜-1，故舍去b=$\sqrt{2}$．
练习册系列答案
相关题目
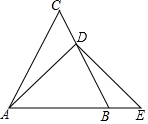如图，等边△ABC中，点D在边BC上，点E在AB的延长线上，且BE=CD，试问：线段DE与AD相等吗？并说明理由．
如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于$\frac{1}{2}$AB长为半径作弧，两弧交于点C．若点C的坐标为（m-1，2n），则m与n的关系为m-1=2n．