题目内容
8．
如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AD于点E，∠BED=65°，∠C=60°，求∠ABC和∠BAC的度数．
分析 由直角三角形的性质求出∠DBE=25°，再由角平分线定义得出∠ABC=2∠DBE=50°，然后由三角形内角和定理求出∠BAC的度数即可．
解答 解：∵AD是BC边上的高，
∴∠ADB=90°，
∴∠DBE+∠BED=90°，
∵∠BED=65°，
∴∠DBE=25°，
∵BE平分∠ABC，
∴∠ABC=2∠DBE=50°，
∵∠BAC+∠ABC+∠C=180°，
∴∠BAC=180°-∠ABC-∠C=180°-50°-60°=70°．
点评 本题考查了三角形内角和定理、角平分线的定义、直角三角形的性质；熟练掌握直角三角形的性质，求出∠ABC的度数是解决问题的关键．
练习册系列答案
每课必练系列答案
相关题目
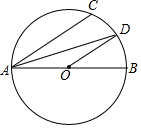如图，AB为⊙O的直径，点C为半圆上一点，AD平分∠CAB交⊙O于点D
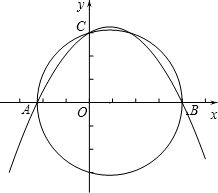如图，在平面直角坐标系xOy中，已知点A（-$\frac{9}{4}$，0），点C（0，3），点B是x轴上一点（位于点A的右侧，以AB为直径的圆恰好经过点C）
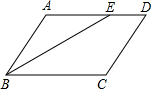如图，在四边形ABCD中，BE平分∠ABC，∠AEB=∠ABE．
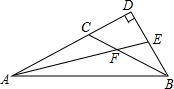如图，在△ABC中，∠CAB=∠ABC=$\frac{1}{4}$∠ACB，AF是∠CAB的平分线，延长AF交AC边上的高BD于点E，求∠AEB的度数．
如图，在△ABC中，∠A=36°，∠ABC=∠ACB
用火柴棒按下列方式搭建三角形：