题目内容
3.如图1,CE平分∠ACD,AE平分∠BAC,且∠EAC+∠ACE=90°.(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,当直角顶点E点移动时,写出∠BAE与∠ECD的数量关系,并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?写出结论,并加以证明.
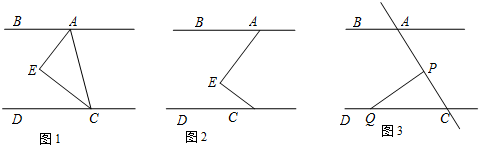
分析 (1)根据角平分线定义得出∠ACD=2∠ACE,∠BAC=2∠EAC,求出∠ACD+∠BAC=180°,根据平行线的判定得出即可;
(2)根据平行线的性质得出∠BAE=∠AFC,求出∠AEC=∠AFC+∠ECD=90°,即可得出答案;
(3)根据平行线的性质得出∠BAC=∠ACG,根据三角形外角性质得出∠ACG=∠CPQ+∠CQP,即可得出答案.
解答 解:(1)AB∥CD,
理由:∵CE平分∠ACD,AE平分∠BAC,
∴∠ACD=2∠ACE,∠BAC=2∠EAC,
又∵∠EAC+∠ACE=90°,
∴∠ACD+∠BAC=180°,
∴AB∥CD;
(2)∠BAE+∠ECD=90°,
理由:延长AE交CD于点F,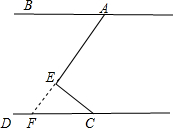
∵AB∥CD,
∴∠BAE=∠AFC,
∵∠AEC是△EFC的一个外角,
∴∠AEC=∠AFC+∠ECD=90°,
∴∠BAE+∠ECD=90°;
(3)∠CPQ+∠CQP=∠BAC,
证明:∵AB∥CD,
∴∠BAC=∠ACG,
∵∠ACG是△PCQ的一个外角,
∴∠ACG=∠CPQ+∠CQP,
∴∠CPQ+∠CQP=∠BAC.
点评 本题考查了平行线的性质和判定,三角形外角性质的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
18.为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加设计比赛,理由是什么?
甲:8,7,10,7,8;
乙:9,5,10,9,7.
(1)将下表填写完整;
| 平 均 数 | 方 差 | |
| 甲 | 8 | 1.2 |
| 乙 | 8 | 3.2 |
 把1$\frac{1}{2}$,-2,π各数及它们的相反数在数轴上表示出来.并用“<”号连接.
把1$\frac{1}{2}$,-2,π各数及它们的相反数在数轴上表示出来.并用“<”号连接. 如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE.
如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E,∠BED=65°,∠C=60°,求∠ABC和∠BAC的度数.
如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E,∠BED=65°,∠C=60°,求∠ABC和∠BAC的度数.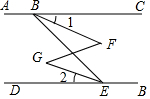
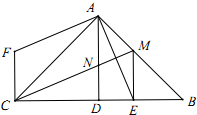 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.