题目内容
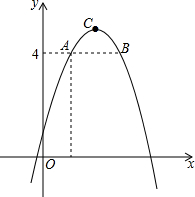 如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式.
如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式.考点:待定系数法求二次函数解析式
专题:
分析:利用待定系数法把点A(1,4)和D(x,4),根据对称轴为x=2,可得x,再根据S△ABC=1,即可得出a,b的值,从而求得函数关系式.
解答:
解:∵二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),
∴对称轴为直线x=2,
即
=2.
解得x=3,
∴点A(1,4),B(3,4),
把A(1,4),B(3,4)代入y=ax2-4ax+b,得-3a+b=4,
∵该函数图象的顶点为C,
∴C(2,b-4a),
∵S△ABC=1,
∴b-4a=2或-2,
解得a=2或6,
∴b=10或22
∴二次函数的解析式为y=2x2-8x+10或y=6x2-24x+22.
∴对称轴为直线x=2,
即
| 1+x |
| 2 |
解得x=3,
∴点A(1,4),B(3,4),
把A(1,4),B(3,4)代入y=ax2-4ax+b,得-3a+b=4,
∵该函数图象的顶点为C,
∴C(2,b-4a),
∵S△ABC=1,
∴b-4a=2或-2,
解得a=2或6,
∴b=10或22
∴二次函数的解析式为y=2x2-8x+10或y=6x2-24x+22.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法,四边形面积的求法等知识,难度中.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图的正方体截去一部分后,剩下的几何体的面数和棱数分别为( )
如图的正方体截去一部分后,剩下的几何体的面数和棱数分别为( )| A、6,13 | B、7,15 |
| C、6,15 | D、7,14 |
地图上的距离为10厘米,这张地图的比例尺为1:100000,则两地的实际距离是( )
| A、100米 |
| B、1000米 |
| C、10000米 |
| D、100000米 |
 如图,边长为a的正六边形内有两个三角形(数据如图),则
如图,边长为a的正六边形内有两个三角形(数据如图),则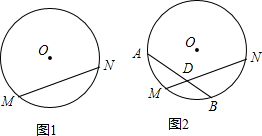 如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
 如图,∠AOB=110°,则∠ACB=
如图,∠AOB=110°,则∠ACB=