题目内容
7.已知x-3y=0,求$\frac{{x}^{2}-2xy+{y}^{2}}{2x+y}÷(x-y)$的值.分析 先对分子因式分解,再化简分式,把x=3y代入计算即可.
解答 解:∵x-3y=0,
∴x=3y,
原式=$\frac{(x-y)^{2}}{2x+y}$•$\frac{1}{x-y}$
=$\frac{x-y}{2x+y}$,
=$\frac{3y-y}{6y+y}$
=$\frac{2}{7}$.
点评 本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
相关题目
17.抛物线y=3x2,y=-3x2,y=x2+3共有的性质是( )
| A. | 开口向上 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x的增大而增大 |
12.下表是2015年6月份的月历表,任意圈出一横行或一竖列相邻的三个数,则这三个数的和不可能是( )
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
| A. | 24 | B. | 43 | C. | 57 | D. | 69 |
16. 如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
 如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )| A. | $\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}+1}{2}$ |
 如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.
如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.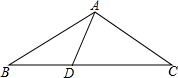 如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.
如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.