题目内容
2.当x=-2时,求$\frac{1}{x+1}-\frac{x+3}{{x}^{2}-1}÷\frac{{x}^{2}+4x+3}{{x}^{2}-2x+1}$的值.分析 先化除法为乘法,然后利用平方差公式、完全平方差公式和十字相乘法对分子、分母进行因式分解,通过约分进行化简.最后代入求值.
解答 解:$\frac{1}{x+1}-\frac{x+3}{{x}^{2}-1}÷\frac{{x}^{2}+4x+3}{{x}^{2}-2x+1}$,
=$\frac{1}{x+1}$-$\frac{x+3}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{(x+1)(x+3)}$,
=$\frac{1}{x+1}$-$\frac{x-1}{(x+1)^{2}}$,
=$\frac{x+1-x+1}{(x+1)^{2}}$,
=$\frac{2}{(x+1)^{2}}$.
把x=-2代入,得
原式=$\frac{2}{(-2+1)^{2}}$=2.
点评 本题考查了分式的化简求值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
13. 如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
 如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )
如图,为估计假山A、B两端的距离,小明在一侧选取了一点C,测得AC=18m,BC=12m,那么AB之间的距离不可能是( )| A. | 12m | B. | 16m | C. | 18m | D. | 30m |
10.下列各式去括号正确的是( )
| A. | a-(b-c)=a-b-c | B. | a+(b-c)=a+b-c | ||
| C. | a2-(a-b+c)=a2-a-b+c | D. | a+2(3a-5)=a+6a-5 |
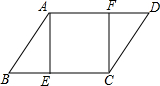 如图,在?ABCD中,∠B=60°,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,BC=2+2$\sqrt{3}$,则AB的长为( )
如图,在?ABCD中,∠B=60°,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,BC=2+2$\sqrt{3}$,则AB的长为( )