题目内容
11.如果多边形的每个内角都比它相邻的外角的4倍多30°,求这个多边形的内角和及对角线的总条数.分析 首先外角为x°,则内角为(4x+30)°,根据内角与相邻的外角是互补关系可得x+4x+30=180,解方程可得x的值,再利用外角和360°÷外角的度数可得边数.
解答 解:设外角为x°,
x+4x+30=180,
解得:x=30,
360°÷30°=12,
∴(12-2)×180=1800°,
∴这个多边形的内角和是1800°,
对角线的总条数=$\frac{(12-3)×12}{2}$=54,
答:这个多边形的内角和是1800°,对角线的总条数是54条.
点评 本题主要考查多边形内角与外角的知识点,此题要结合多边形的内角和公式寻求等量关系,构建方程求解即可.从n边形一个顶点可以引n-3条对角线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知9m÷32m+2=$(\frac{1}{3})$n,n的值是( )
| A. | -2 | B. | 2 | C. | 0.5 | D. | -0.5 |
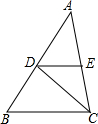 如图,CD平分∠ACB,DE∥BC,∠AED=76°,求∠EDC的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=76°,求∠EDC的度数.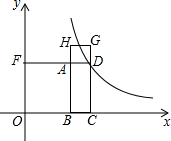 已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.
已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.