题目内容
10.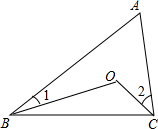 如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )
如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )| A. | 45° | B. | 55° | C. | 135° | D. | 150° |
分析 先根据三角形内角和定理求出∠OBC+∠OCB的度数,再根据∠BOC+(∠OBC+∠OCB)=180°即可得出结论.
解答 解:∵∠A=80°,∠1=15°,∠2=40°,
∴∠OBC+∠OCB=180°-∠A-∠1-∠2=180°-80°-15°-40°=45°,
∵∠BOC+(∠OBC+∠OCB)=180°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-45°=135°.
故选C.
点评 此题主要考查了三角形内角与外角的关系,关键是掌握三角形内角与外角的关系定理.

练习册系列答案
相关题目
18.在$\sqrt{6}$,0,-2,3这四个数中,最大的数是( )
| A. | $\sqrt{6}$ | B. | 0 | C. | -2 | D. | 3 |
20.东方学校将为2013级新生购置课桌椅,从批发地运到学校有火车和汽车两种运输工具,运输过程中的损耗均为160元/时,其他主要参考数据如下:
(1)如果从批发地运到学校有400千米,请问汽车和火车的总支出费用各是多少?
(2)若两种运输工具的费用相等,你知道批发地到学校之间的路程是多少千米吗?请你用方程解答;
(3)如果从批发地到学校的距离为S,选择哪种运输工具比较合算呢?
| 运输工具 | 平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
| 火车 | 100 | 18 | 1800 |
| 汽车 | 80 | 22 | 1000 |
(2)若两种运输工具的费用相等,你知道批发地到学校之间的路程是多少千米吗?请你用方程解答;
(3)如果从批发地到学校的距离为S,选择哪种运输工具比较合算呢?
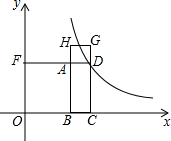 已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.
已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.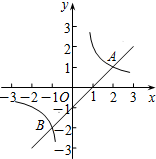 如图,直线y=x+m与双曲线y=$\frac{k}{x}$相交于A(2,1)、B两点.
如图,直线y=x+m与双曲线y=$\frac{k}{x}$相交于A(2,1)、B两点. 如图,AB∥CD,AD∥BC,AC与BD相交于点O,点E、O、F三点在同一条直线上,则图中全等三角形的组数是6对.
如图,AB∥CD,AD∥BC,AC与BD相交于点O,点E、O、F三点在同一条直线上,则图中全等三角形的组数是6对. 如图,每个小正方形的边长都为1.
如图,每个小正方形的边长都为1.