题目内容
18.有一拦水坝的横截面是等腰梯形,它的上底为6米,下底为10米,高为2米,那么拦水坝斜坡的坡度和坡角分别是( )| A. | $\frac{\sqrt{3}}{3}$,60° | B. | 1,45° | C. | $\sqrt{3}$,60° | D. | $\frac{\sqrt{3}}{3}$,30° |
分析 从上底两个顶点向下底引垂线,构造出两个直角三角形和一个矩形,利用等腰梯形的性质得到DF长,进而得到坡度、坡角.
解答 解:如图,作AF⊥CD于F,BE⊥CD于E.
AB=6m,DC=10m,AF=BE=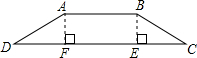 2m,
2m,
∵AF⊥DC,BE⊥DC,四边形ABCD为等腰梯形.
∴四边形AFEB是矩形,△ADF≌△BCE,
∴AB=EF=6m,
∴DF=EC=$\frac{1}{2}$(BC-AD)=$\frac{1}{2}$(10-6)=2m,
∵tanD=$\frac{AF}{DF}$=$\frac{2}{2}$=1.
∴坡度是1:1,
∵tanD=$\frac{AF}{DF}$=1,
∴∠D=45°,
故选B.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,根据题意画出图形,作出辅助线,利用数形结合求解是解答此题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
 在所给数轴上画出表示数-3,-1,|-2|,-(-4),|0|,-|-5|的点,把这组数从小到大用”<“号连接起来.
在所给数轴上画出表示数-3,-1,|-2|,-(-4),|0|,-|-5|的点,把这组数从小到大用”<“号连接起来. 如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.
如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.
 已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形.
已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形.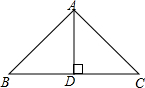 如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2
如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2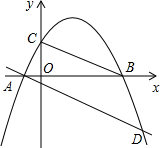 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.