题目内容
9.已知:2$\overrightarrow{a}$+2$\overrightarrow{b}$=3$\overrightarrow{c}$.3$\overrightarrow{a}$-$\overrightarrow{b}$=2$\overrightarrow{c}$(1)用向量$\overrightarrow{b}$表示向量$\overrightarrow{a}$;
(2)向量$\overrightarrow{a}$与$\overrightarrow{b}$是否平行?简要说明理由.
分析 (1)由2$\overrightarrow{a}$+2$\overrightarrow{b}$=3$\overrightarrow{c}$,3$\overrightarrow{a}$-$\overrightarrow{b}$=2$\overrightarrow{c}$,消去$\overrightarrow{c}$,即可求得向量$\overrightarrow{a}$与$\overrightarrow{b}$的关系;
(2)由(1)中,向量$\overrightarrow{a}$与$\overrightarrow{b}$的关系,可得向量$\overrightarrow{a}$与$\overrightarrow{b}$平行或共线.
解答 解:(1)∵2$\overrightarrow{a}$+2$\overrightarrow{b}$=3$\overrightarrow{c}$①,3$\overrightarrow{a}$-$\overrightarrow{b}$=2$\overrightarrow{c}$②,
∴②×3-①×2,得:5$\overrightarrow{a}$-7$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$=$\frac{7}{5}$$\overrightarrow{b}$;
(2)不一定平行.
理由:∵$\overrightarrow{a}$=$\frac{7}{5}$$\overrightarrow{b}$,
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$平行或共线.
点评 此题考查了平面向量的知识.注意理解平行向量的定义.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
18.有一拦水坝的横截面是等腰梯形,它的上底为6米,下底为10米,高为2米,那么拦水坝斜坡的坡度和坡角分别是( )
| A. | $\frac{\sqrt{3}}{3}$,60° | B. | 1,45° | C. | $\sqrt{3}$,60° | D. | $\frac{\sqrt{3}}{3}$,30° |
 已知等边△ABC,请做出旋转后的三角形.
已知等边△ABC,请做出旋转后的三角形.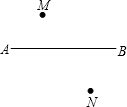 如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近;汽车行驶到点Q时,离村庄N最近;汽车行驶到H点时,它到M、N两村庄的距离之和最短.请在图中公路AB上分别画出点P、Q的位置.
如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路AB两侧的村庄.设汽车行驶到点P时,离村庄M最近;汽车行驶到点Q时,离村庄N最近;汽车行驶到H点时,它到M、N两村庄的距离之和最短.请在图中公路AB上分别画出点P、Q的位置.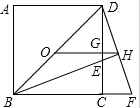 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
 如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.
如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.