题目内容
7.过平行四边形ABCD的顶点A、C分别作对角线BD的垂线,垂足是E、F,则四边形AECF是( )| A. | 任意四边形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
分析 可先依据题意作出简单的图形,则在平行四边形ABCD中,不难得出△ABE≌△CDF,得出AE=CF,再由垂直关系得出AE∥CF,进而可得出四边形AECF一定是平行四边形.
解答 解:如图所示,
在平行四边形ABCD中,则可得AB=CD,∠ABE=∠CDF,
又AE⊥BD,CF⊥BD,
∴AE∥CF,
在△ABE和△CDF中
∵$\left\{\begin{array}{l}{∠AEB=∠CFD}\\{∠EBA=∠FDC}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
故选:B.
点评 本题主要考查了平行四边形的性质及全等三角形的判定及性质问题,利用全等三角形的判定方法得出△ABE≌△CDF是解题关键.

练习册系列答案
相关题目
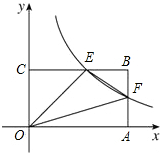 如图,双曲线y=$\frac{4}{x}$(x>0)与矩形OABC的边CB、BA分别交于点E、F,且AF=BF,连接EF,则△OEF的面积为3.
如图,双曲线y=$\frac{4}{x}$(x>0)与矩形OABC的边CB、BA分别交于点E、F,且AF=BF,连接EF,则△OEF的面积为3.